Question

如图，已知：AB=AC，直线m经过点A，点D、E是直线m上两个动点，连接BD、CE．

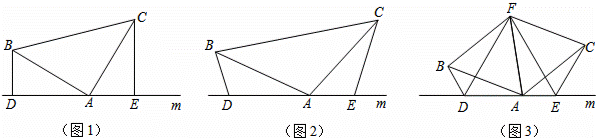
（1）如图1，若∠BAC=90°，BD⊥DE，CE⊥DE．求证：DE=BD+CE．

（2）如图2，若∠BAC=∠BDA=∠AEC，则（1）中的结论DE=BD+CE还成立吗？（只回答答案，不用证明）

（3）如图3，在（2）的条件下，点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，是判定△DEF的形状，并证明你的判定．

Answer 1

解：（1）∵∠BAC=90°，∴∠BAD+∠CAE=90°,∵BD⊥AD，∴∠BDA=90°，

∴∠BAD+∠ABD=90°，∴∠DBA=∠CAE；　　　∵CE⊥DE，∴∠CEA=90°，

∴∠ADB=∠CEA．

在△ADB和△CEA中，

，∴△ADB≌△CEA（AAS）∴AD=CE，BD=AE．

∵DE=DA+AE，∴DE=BD+CE；

（2）（1）中的结论DE=BD+CE仍然成立．　

理由：∵∠DAB+BAC+∠CAE=180°，∠CAE+∠ACE+∠AEC=180°，

∴∠DAB+∠BAC+∠CAE=∠CAE+∠ACE+∠AEC．∵∠BAC=∠AEC，∴∠DAB=∠ACE．

在△ADB和△CEA中

，∴△ADB≌△CEA（AAS）∴AD=CE，BD=AE．∵DE=DA+AE，

∴DE=BD+CE；

（3）△DFE是等边三角形．

理由：∵△ADB≌△CEA，∴∠DBA=∠EAC，BD=EA．∵△ABF和△ACF均为等边三角形，∴BF=AB=AF=AC=CF，∠ABF=∠CAF=60°，∴∠ABF+∠DBA=∠CAF+∠EAC，

∴∠DBF=∠EAF．

在△FDB和△FEA中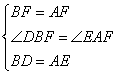，，∴△FDB≌△FEA（SAS），∴DF=EF，∠DFB=∠EFA．∵∠DFB+∠DFA=60°，∴∠EFA+∠DFA=60°，即∠DFE=60°

∴△DFE是等边三角形．