题目内容
 如图,直线l:y=
如图,直线l:y=| 3 |
| 4 |
(1)点A坐标是
(2)当点P在什么位置时,△APQ≌△CBP,说明理由.
(3)在(2)的条件下,可得点Q的横坐标为-
| 16 |
| 5 |
考点:一次函数综合题
专题:
分析:(1)把x=0和y=0分别代入一次函数的解析式,求出A、B的坐标,根据勾股定理求出BC即可.
(2)求出∠PAQ=∠BCP,∠AQP=∠BPC,根据点的坐标求出AP=BC,根据全等三角形的判定推出即可.
(3)先找到B点关于x轴对称的点B′的坐标,把点Q的横坐标为-
代入直线l可得点Q的坐标,再根据待定系数法可得直线B′Q的解析式,把y=0代入该函数的解析式,即可求出点M的坐标.
(2)求出∠PAQ=∠BCP,∠AQP=∠BPC,根据点的坐标求出AP=BC,根据全等三角形的判定推出即可.
(3)先找到B点关于x轴对称的点B′的坐标,把点Q的横坐标为-
| 16 |
| 5 |
解答:解:(1)∵y=
x+6
∴当x=0时,y=6,
当y=0时,x=-8,
即点A的坐标是(-8,0),点B的坐标是(0,6),
∵C点与A点关于y轴对称,
∴C的坐标是(8,0),
∴OA=8,OC=8,OB=6,
由勾股定理得:BC=
=10,
(2)当P的坐标是(2,0)时,△APQ≌△CBP,
理由是:∵OA=8,P(2,0),
∴AP=8+2=10=BP,
∵∠BPQ=∠BAO,∠BAO+∠AQP+∠APQ=180°,∠APQ+∠BPQ+∠BPC=180°,
∴∠AQP=∠BPC,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
在△APQ和△CBP中,
,
∴△APQ≌△CBP(AAS),
∴当P的坐标是(2,0)时,△APQ≌△CBP.
(3)B点关于x轴对称的点B′的坐标为(0,-6),
把点Q的横坐标为-
代入直线l可得y=
×(-
)+6=
,
则点Q的坐标为(-
,
),
设直线B′Q的解析式为y=kx+b,则
,
解得
,
故直线B′Q的解析式为y=-3x-6,
把y=0代入y=-3x-6可得0=-3x-6,解得x=-2,
故点M的坐标为(-2,0).
故答案为:(-8,0),(0,6),10.
| 3 |
| 4 |
∴当x=0时,y=6,
当y=0时,x=-8,
即点A的坐标是(-8,0),点B的坐标是(0,6),
∵C点与A点关于y轴对称,
∴C的坐标是(8,0),
∴OA=8,OC=8,OB=6,
由勾股定理得:BC=
| 62+82 |
(2)当P的坐标是(2,0)时,△APQ≌△CBP,
理由是:∵OA=8,P(2,0),
∴AP=8+2=10=BP,
∵∠BPQ=∠BAO,∠BAO+∠AQP+∠APQ=180°,∠APQ+∠BPQ+∠BPC=180°,
∴∠AQP=∠BPC,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
在△APQ和△CBP中,
|
∴△APQ≌△CBP(AAS),
∴当P的坐标是(2,0)时,△APQ≌△CBP.
(3)B点关于x轴对称的点B′的坐标为(0,-6),
把点Q的横坐标为-
| 16 |
| 5 |
| 3 |
| 4 |
| 16 |
| 5 |
| 18 |
| 5 |
则点Q的坐标为(-
| 16 |
| 5 |
| 18 |
| 5 |
设直线B′Q的解析式为y=kx+b,则
|
解得
|
故直线B′Q的解析式为y=-3x-6,
把y=0代入y=-3x-6可得0=-3x-6,解得x=-2,
故点M的坐标为(-2,0).
故答案为:(-8,0),(0,6),10.
点评:本题考查了一次函数图象上点的坐标特征,勾股定理,轴对称最短路线,全等三角形的性质和判定的应用,题目综合性比较强,难度偏大.

练习册系列答案
相关题目
 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与函数
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与函数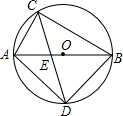 如图,已知⊙O中,AB为直径,AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于D.
如图,已知⊙O中,AB为直径,AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于D.