题目内容
已知:如图1,直线y=
x与双曲线y=
交于A,B两点,且点A的坐标为(6,m).
(1)求双曲线y=
的解析式;
(2)点C(n,4)在双曲线y=
上,求△AOC的面积;
(3)过原点O作另一条直线l与双曲线y=
交于P,Q两点,且点P在第一象限.若由点A,P,B,Q为顶点组成的四边形的面积为20,请直接写出所有符合条件的点P的坐标.

| 1 |
| 3 |
| k |
| x |
(1)求双曲线y=
| k |
| x |
(2)点C(n,4)在双曲线y=
| k |
| x |
(3)过原点O作另一条直线l与双曲线y=
| k |
| x |

分析:(1)首先利用正比例函数解析式计算出A点坐标,再把A点坐标代入反比例函数y=
,可得反比例函数解析式;
(2)分别过点C,A作CD⊥x轴,AE⊥x轴,再利用反比例函数解析式计算出点C的坐标,根据反比例函数解析式计算出S△CDO=S△AEO=
|k|,再用S△AOC=S四边形COEA-S△AOE=S四边形COEA-S△COD=S梯形CDEA,即可算出答案;
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即为5.可根据双曲线的解析式设出P点的坐标,然后参照(2)的三角形面积的求法表示出△POA的面积,由于△POA的面积为5,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
| k |
| x |
(2)分别过点C,A作CD⊥x轴,AE⊥x轴,再利用反比例函数解析式计算出点C的坐标,根据反比例函数解析式计算出S△CDO=S△AEO=
| 1 |
| 2 |
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即为5.可根据双曲线的解析式设出P点的坐标,然后参照(2)的三角形面积的求法表示出△POA的面积,由于△POA的面积为5,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
解答:解:(1)∵点A(6,m)在直线y=
x上,
∴m=
×6=2,
∴A(6,2),
∵点A(6,2)在双曲线y=
上,
∴2=
,
解得:k=12.
故双曲线的解析式为y=
;
(2)分别过点C,A作CD⊥x轴,AE⊥x轴,
垂足分别为点D,E.(如图1)
∵点C(n,4)在双曲线y=
上,
∴4=
,
解得:n=3,
即点C的坐标为(3,4),
∵点A,C都在双曲线y=
上,
∴S△AOE=S△COD=
×12=6.
∴S△AOC=S四边形COEA-S△AOE=S四边形COEA-S△COD=S梯形CDEA,
∴S△AOC=
(CD+AE)•DE=
×(4+2)×(6-3)=9;
(3))∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=
S平行四边形APBQ=
×20=5,
设点P的横坐标为m(m>0且m≠6),
得P(m,
),
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=6,
若0<m<6,如图,
∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=5.
∴
(2+
)•(6-m)=5.
∴m=4,m=-9(舍去),
∴P(4,3);
若m>6,如图,
∵S△AOF+S梯形AFEP=S△AOP+S△POE,
∴S梯形PEFA=S△POA=5.
∴
(2+
)•(m-6)=5,
解得m=9,m=-5(舍去),
∴P(9,
).
故点P的坐标是:P(4,3)或P(9,
).
| 1 |
| 3 |
∴m=
| 1 |
| 3 |
∴A(6,2),
∵点A(6,2)在双曲线y=
| k |
| x |
∴2=
| k |
| 6 |
解得:k=12.
故双曲线的解析式为y=
| 12 |
| x |

(2)分别过点C,A作CD⊥x轴,AE⊥x轴,
垂足分别为点D,E.(如图1)
∵点C(n,4)在双曲线y=
| 12 |
| x |
∴4=
| 12 |
| n |
解得:n=3,
即点C的坐标为(3,4),
∵点A,C都在双曲线y=
| 12 |
| x |
∴S△AOE=S△COD=
| 1 |
| 2 |
∴S△AOC=S四边形COEA-S△AOE=S四边形COEA-S△COD=S梯形CDEA,
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
(3))∵反比例函数图象是关于原点O的中心对称图形,

∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=
| 1 |
| 4 |
| 1 |
| 4 |
设点P的横坐标为m(m>0且m≠6),
得P(m,
| 12 |
| m |
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=6,
若0<m<6,如图,
∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=5.
∴
| 1 |
| 2 |
| 12 |
| m |

∴m=4,m=-9(舍去),
∴P(4,3);
若m>6,如图,
∵S△AOF+S梯形AFEP=S△AOP+S△POE,
∴S梯形PEFA=S△POA=5.
∴
| 1 |
| 2 |
| 12 |
| m |
解得m=9,m=-5(舍去),
∴P(9,
| 4 |
| 3 |
故点P的坐标是:P(4,3)或P(9,
| 4 |
| 3 |
点评:本题考查了反比例解析式的确定和性质、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.难点是不规则图形的面积通常转化为规则图形的面积的和差来求解.

练习册系列答案
相关题目
 已知:如图,同一直线上有四点B、E、C、F,且∠A=∠D,∠B=∠DEF,BE=CF.
已知:如图,同一直线上有四点B、E、C、F,且∠A=∠D,∠B=∠DEF,BE=CF.
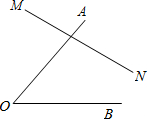 已知:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等(要求写出作法,并保留作图痕迹,写出结论)
已知:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等(要求写出作法,并保留作图痕迹,写出结论)