题目内容
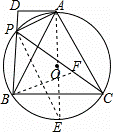
如图,A,P,B,C是⊙O上的四个点,∠APC=∠BPC=60°,过点A作⊙O的切线交BP的延长线于点D.

(1)求证:△ADP∽△BDA;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)若AD=2,PD=1,求线段BC的长.
1)证明见解析;(2) PA+PB=PC,证明见解析;(3) .
.
【解析】(1)作⊙O的直径AE,连接PE,∵AE是⊙O的直径,AD是⊙O的切线,
∴∠DAE=∠APE=90°,∴∠PAD+∠PAE=∠PAE+∠E=90°,∴∠PAD=∠E,∵∠PBA=∠E,∴∠PAD=∠PBA,∵∠PAD=∠PBA,∠ADP=∠BDA,∴△ADP∽△BDA;
(2)PA+PB=PC,
证明:在线段PC上截取PF=PB,连接BF,∵PF=PB,∠BPC=60°,∴△PBF是等边三角形,∴PB=BF,∠BFP=60°,∴∠BFC=180°﹣∠PFB=120°,∵∠BPA=∠APC+∠BPC=120°,∴∠BPA=∠BFC,在△BPA和△BFC中,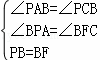 ,∴△BPA≌△BFC(AAS),∴PA=FC,A
,∴△BPA≌△BFC(AAS),∴PA=FC,A B=BC,∴PA+PB=PF+FC=PC;
B=BC,∴PA+PB=PF+FC=PC;
(3)∵△ADP∽△BDA,∴ =
=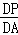 =
=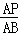 ,∵AD=2,PD=1∴BD=4,AB=2AP,∴BP=BD﹣DP=3,
,∵AD=2,PD=1∴BD=4,AB=2AP,∴BP=BD﹣DP=3,
∵∠APD=180°﹣∠BPA=60° ,∴∠APD=∠APC,∵∠PAD=∠E,∠PCA=∠E,∴PAD=∠PCA,∴△ADP∽△CAP,∴
,∴∠APD=∠APC,∵∠PAD=∠E,∠PCA=∠E,∴PAD=∠PCA,∴△ADP∽△CAP,∴ =
=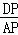 ,∴AP2=CP•PD,∴AP2=(3+AP)•1,
,∴AP2=CP•PD,∴AP2=(3+AP)•1,
解得:AP= 或AP=
或AP=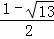 (舍去),∴BC=AB=2AP=1+
(舍去),∴BC=AB=2AP=1+ .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 ,则一次函数
,则一次函数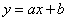 与反比例函数
与反比例函数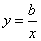 在同一直角坐标系中的图象大致可能是( )
在同一直角坐标系中的图象大致可能是( ) B.
B. C.
C. D.
D.
 中,
中, ,以点
,以点 为圆心,
为圆心, 为半径的圆弧交
为半径的圆弧交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,
,
 则图中阴影部分的面积为 .(结果保留
则图中阴影部分的面积为 .(结果保留 )
)
 、
、 、
、 、… ,按如图所示的方式放置.点
、… ,按如图所示的方式放置.点 、
、 、
、 、…和点
、…和点 、
、 、
、 、…分别在直线
、…分别在直线 和
和 轴上,则第2015个正方形
轴上,则第2015个正方形 的边长为_____________.
的边长为_____________.
 分别与AB,CD相交,若∠1=120°,则∠2等于( )
分别与AB,CD相交,若∠1=120°,则∠2等于( )
 有意义的x的取值范围是( )
有意义的x的取值范围是( ) B.x<7且x
B.x<7且x C.x
C.x 7且x
7且x D.x
D.x
 与
与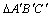 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.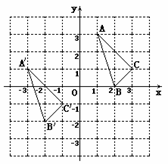
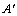 ;
; 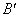 ;
;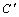 ;
; (3)若点
(3)若点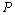 (
(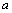 ,
,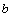 )是
)是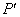 的坐标为 ;
的坐标为 ;