��Ŀ����
���������ߵij��ֱ���8��6�������ߵij���һԪ���η���x2��16x+60=0��һ��ʵ��������������ε�����ǣ� ��
A. 24 B. 24��8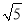 C. 48 D. 8
C. 48 D. 8
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
���������ߵij��ֱ���8��6�������ߵij���һԪ���η���x2��16x+60=0��һ��ʵ��������������ε�����ǣ� ��
A. 24 B. 24��8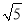 C. 48 D. 8
C. 48 D. 8