题目内容
20.已知实数x,y满足$\sqrt{2x-3y-1}$+|x-2y+2|=0,则2x-$\frac{4}{5}$y的平方根为±2$\sqrt{3}$.分析 利用非负数的性质列出方程组,求出方程组的解得到x与y的值,即可确定出原式的平方根.
解答 解:∵$\sqrt{2x-3y-1}$+|x-2y+2|=0,
∴$\left\{\begin{array}{l}{2x-3y=1}\\{x-2y=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=5}\end{array}\right.$,
则2x-$\frac{4}{5}$y=16-4=12,12的平方根为±2$\sqrt{3}$,
故答案为:±2$\sqrt{3}$
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.下列各数精确到万分位的是( )
| A. | 0.0720 | B. | 0.072 | C. | 0.72 | D. | 0.176 |
9.下列说法中正确的是( )
| A. | 两个全等三角形成轴对称 | |
| B. | 两个三角形关于某直线对称,不一定全等 | |
| C. | 线段AB的对称轴垂直平分AB | |
| D. | 直线MN垂直平分线段AB,则直线MN是线段AB的对称轴 |
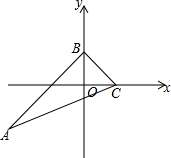 如图,△ABC的三条内角平分线交点在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为y=$\frac{1}{2}$x-1,则tanA的值是$\frac{1}{3}$.
如图,△ABC的三条内角平分线交点在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为y=$\frac{1}{2}$x-1,则tanA的值是$\frac{1}{3}$.



