题目内容
1.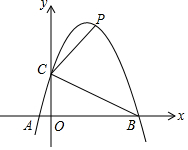 已知抛物线y=ax2-2ax+m与x轴交于A(-1,0)、B(x2,0)两点,与y轴正半轴交于点C,且满足S△ABC=4.
已知抛物线y=ax2-2ax+m与x轴交于A(-1,0)、B(x2,0)两点,与y轴正半轴交于点C,且满足S△ABC=4.(1)求此抛物线的解析式;
(2)过点O的直线交BC于D,且OD刚好平分△ABC的面积,求点D的坐标;
(3)在第一象限的抛物线上是否存在点P,使得∠PCA+∠ABC=180°?若存在,请你求出P点的坐标;若不存在,请说明理由.
分析 (1)把A(-1,0)的坐标代入y=ax2-2ax+m,得a+2a+m=0,可得m=-3a,所以抛物线的解析式为y=ax2-2ax-3a,令y=0,ax2-2ax+-3a=0,解得x=-1或3,推出B(3,0),AB=4,根据S△ABC=4,可得OC=2,即可求出a的值解决问题.
(2)如图1中,连接AC,设D(m,n).由题意S△BOD=$\frac{1}{2}$S△ABC,可得$\frac{1}{2}$×3×n=2,推出n=$\frac{4}{3}$,求出直线BC的解析式为y=-$\frac{2}{3}$x+2,即可求出点D坐标.
(3)如图2中,连接AC,延长PC交x轴于E,设E(m,0).由△ECA∽△EBC,得到EC2=EA•EB,可得方程m2+4=(-1-m)(3-m),求出点E坐标,再求出直线PC的解析式,利用方程组求交点坐标即可.
解答 解:(1)把A(-1,0)的坐标代入y=ax2-2ax+m,得a+2a+m=0,
∴m=-3a,
∴抛物线的解析式为y=ax2-2ax-3a,令y=0,ax2-2ax+-3a=0,解得x=-1或3,
∴B(3,0),AB=4,
∵S△ABC=4,
∴$\frac{1}{2}$×4×OC=4,
∴OC=2,
∴-3a=2,
∴a=-$\frac{2}{3}$,
∴抛物线的解析式为y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2.
(2)如图1中,连接AC,设D(m,n).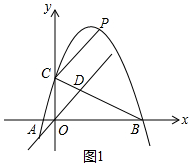
由题意S△BOD=$\frac{1}{2}$S△ABC,
∴$\frac{1}{2}$×3×n=2,
∴n=$\frac{4}{3}$,
∵B(3,0),C(0,2),
设直线BC的解析式为y=kx+b则有$\left\{\begin{array}{l}{b=2}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=2}\end{array}\right.$,
∴直线BC的解析式为y=-$\frac{2}{3}$x+2,
当y=$\frac{4}{3}$,$\frac{4}{3}$=-$\frac{2}{3}$x+2,
∴x=1,
∴D(1,$\frac{4}{3}$).
(3)如图2中,连接AC,延长PC交x轴于E,设E(m,0).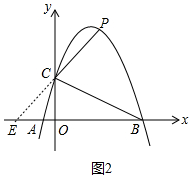
∵∠PCA+∠ABC=180°,∠PCA+∠ECA=180°,
∴∠ECA=∠EBC,∵∠CEA=∠CEB,
∴△ECA∽△EBC,
∴EC2=EA•EB,
∴m2+4=(-1-m)(3-m),
∴m=-$\frac{7}{2}$,
∴E(-$\frac{7}{2}$,0),
∴直线PC的解析式为y=$\frac{4}{7}$x+2,
由$\left\{\begin{array}{l}{y=\frac{4}{7}x+2}\\{y=-\frac{2}{3}{x}^{2}+\frac{4}{3}x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{7}{2}}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{8}{7}}\\{y=\frac{130}{49}}\end{array}\right.$.
点评 本题考查二次函数综合题、一次函数的应用、相似三角形的判定和性质、三角形的面积、勾股定理等知识,解题的关键是学会用方程的思想思考问题,学会添加辅助线,构造相似三角形解决问题,属于中考压轴题.

| A. | 45 | B. | $\frac{1}{45}$ | C. | $\frac{1}{5}$ | D. | 5 |
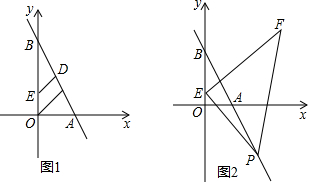
 根据图中数据可求阴影部分的面积和为( )
根据图中数据可求阴影部分的面积和为( )| A. | 12 | B. | 10 | C. | 8 | D. | 7 |
| A. | 所有的矩形都相似 | |
| B. | 所有的直角三角形都相似 | |
| C. | 有一个角是50°的所有等腰三角形都相似 | |
| D. | 有一个角是100°的所有等腰三角形都相似 |
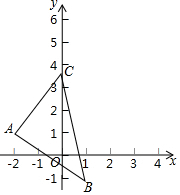 在平面直角坐标系中,A(-2,1),B(1,-1),C在y轴上,S△ABC=8,求点C的坐标.
在平面直角坐标系中,A(-2,1),B(1,-1),C在y轴上,S△ABC=8,求点C的坐标. 已知数轴上有三点A、B、C.
已知数轴上有三点A、B、C.