题目内容
10.若x的方程kx2-$\sqrt{3k+1}$x+3=0有两实数根,则k的取值范围为k≤$\frac{1}{9}$且k≠0.分析 关于x的方程kx2-$\sqrt{3k+1}$x+3=0有两个实数根,即判别式△=b2-4ac≥0.且k≠0,即可得到关于k的不等式,从而求得k的范围.
解答 解:∵方程kx2-$\sqrt{3k+1}$x+3=0有两实数根,
∴△≥0,即(-$\sqrt{3k+1}$)2-4×k×3≥0,且k≠0,
解得:k≤$\frac{1}{9}$,且k≠0,
故答案为:k≤$\frac{1}{9}$且k≠0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
20.已知方程4ax-2x+1=-3的解为x=1,那么2a+$\frac{1}{a}$的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -3 | D. | 3 |
19.一元二次方程2x2+5x+3=0根的判别式的值是( )
| A. | 1 | B. | -1 | C. | 13 | D. | 19 |
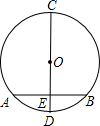 如图,在⊙O中,已知CD是直径,AB是弦,CD⊥AB,垂足为E.
如图,在⊙O中,已知CD是直径,AB是弦,CD⊥AB,垂足为E. 如图,△ABC中,∠ACB=90°,AC=12,BC=16.点P从A点出发沿A-C-B路径向终点B运动;点Q从点B出发沿B-C-A路径向终点A运动.点P和Q分别以2和6的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒.当t=1或者3.5或12秒时,△PEC与△QFC全等.
如图,△ABC中,∠ACB=90°,AC=12,BC=16.点P从A点出发沿A-C-B路径向终点B运动;点Q从点B出发沿B-C-A路径向终点A运动.点P和Q分别以2和6的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒.当t=1或者3.5或12秒时,△PEC与△QFC全等.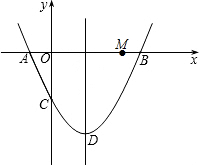 如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,顶点是D,且点A坐标为(-1,0),点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,m的值是$\frac{4}{17}$.
如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,顶点是D,且点A坐标为(-1,0),点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,m的值是$\frac{4}{17}$.