题目内容
如图，AB为半圆O的直径，C为AO的中点，CD⊥AB交半圆于点D，以C为圆心，CD为半径画弧DE交AB于E点，若AB=8cm，则图中阴影部分的面积为 cm2．（取准确值）
【答案】分析：阴影部分的面积=S半圆-（SADC+S扇形CDE）=S半圆-（S扇形OAD-S△CDO+S扇形CDE）．
解答：
解：连接AD，OD，BD，可得△ACD∽△CDB，有CD2=AC•CB，
∴CD=2
cm，OC=2cm，tan∠COD=2
：2=
：1，
∴∠AOD=60°，即△AOD是等边三角形，
∴S扇形OAD=
=
cm2，S△CDO=
CO•CD=2
cm2．
∴SADC=S扇形OAD-S△CDO=（
-2
）cm2，S扇形CDE=
×π（2
）2=3πcm2．
∴阴影部分的面积=S半圆-（SADC+S扇形CDE）=（
+2
）cm2．
故答案为：（
+2
）
点评：本题利用了相似三角形的性质，等边三角形的性质，三角形的面积公式，圆的面积公式，扇形的面积公式求解．
解答：
解：连接AD，OD，BD，可得△ACD∽△CDB，有CD2=AC•CB，∴CD=2
cm，OC=2cm，tan∠COD=2：2=：1，∴∠AOD=60°，即△AOD是等边三角形，
∴S扇形OAD=
=cm2，S△CDO=CO•CD=2cm2．∴SADC=S扇形OAD-S△CDO=（
-2）cm2，S扇形CDE=×π（2）2=3πcm2．∴阴影部分的面积=S半圆-（SADC+S扇形CDE）=（
+2）cm2．故答案为：（
+2）点评：本题利用了相似三角形的性质，等边三角形的性质，三角形的面积公式，圆的面积公式，扇形的面积公式求解．
练习册系列答案
全能测控期末小状元系列答案
相关题目
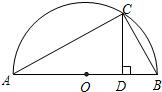为D，AD=a，DB=b．
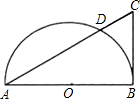如图，AB为半圆O的直径，CB切半圆于点B，AC交半圆于点D，若CD=1，AD=3，则⊙O半径的长为
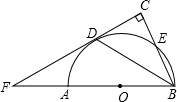C，直线CD交BA的延长线于点F．
如图，AB为半圆O的直径，B1，B2，…，Bk是半圆上的k个点，满足BB1=B1B2=…Bk-1Bk，对于线段OB1，OB2，…，OBk，AB1，AB2，…，ABk，当k=4时，有