题目内容
12.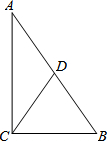 如图,△ABC中,∠ACB=90°,∠B=55°,点D是斜边AB的中点,那么∠ACD的度数为( )
如图,△ABC中,∠ACB=90°,∠B=55°,点D是斜边AB的中点,那么∠ACD的度数为( )| A. | 15° | B. | 25° | C. | 35° | D. | 45° |
分析 先根据在直角三角形中,斜边上的中线等于斜边的一半,得出CD=BD,进而得到∠B=∠DCB=55°,再根据∠ACB=90°,即可得出∠ACD的度数.
解答 解:∵△ABC中,∠ACB=90°,点D是斜边AB的中点,
∴CD=BD=$\frac{1}{2}$AB,
∴∠B=∠DCB=55°,
又∵∠ACB=90°,
∴∠ACD=90°-55°=35°,
故选:C.
点评 本题主要考查了直角三角形斜边上中线的性质,解题时注意:在直角三角形中,斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
3.下列运算正确的是( )
| A. | m2•n2=(mn)4 | B. | 5x2y-4x2y=1 | C. | m-2=$\frac{1}{{m}^{2}}$(m≠0) | D. | (m-n)2=m2-n2 |
4.下列图形中,正方体展开后得到的图形不可能是( )
| A. |  | B. |  | C. |  | D. |  |
6.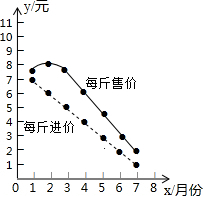 1-7月份,某种蔬菜每斤的进价与每斤的售价的信息如图所示,则出售该种蔬菜每斤利润最大的月份是( )
1-7月份,某种蔬菜每斤的进价与每斤的售价的信息如图所示,则出售该种蔬菜每斤利润最大的月份是( )
 1-7月份,某种蔬菜每斤的进价与每斤的售价的信息如图所示,则出售该种蔬菜每斤利润最大的月份是( )
1-7月份,某种蔬菜每斤的进价与每斤的售价的信息如图所示,则出售该种蔬菜每斤利润最大的月份是( )| A. | 3月份 | B. | 4月份 | C. | 5月份 | D. | 6月份 |
 如图,数轴上有A、B、C、D四点,根据图中各点的位置,所表示的数与5-$\sqrt{11}$最接近的点是( )
如图,数轴上有A、B、C、D四点,根据图中各点的位置,所表示的数与5-$\sqrt{11}$最接近的点是( )