Question

【题目】在△中，已知是边的中点，是△的重心，过点的直线分别交、于点、.

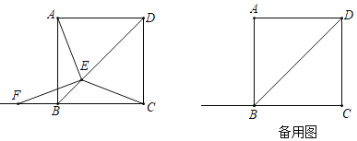
（1）如图1，当∥时，求证：；

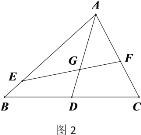
（2）如图2，当和不平行，且点、分别在线段、上时，（1）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由.

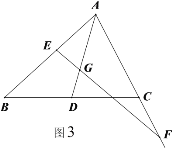
（3）如图3，当点在的延长线上或点在的延长线上时，（1）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由.

Answer 1

【答案】（1）证明见解析；（2）（1）中结论成立，理由见解析；（3）（1）中结论不成立，理由见解析.

【解析】

（1）根据G为重心可知，由EF∥BC可知,，故

（2）过点作∥交的延长线于点，、的延长线相交于点，则，，故要求式子，又，D是的中点，即，故有，所以原式，又有，得，故结论成立；

（3）由G点为重心可知，当点与点重合时，为中点，，故当点在的延长线上时，，,则，同理：当点在的延长线上时，，故结论不成立.

（1）证明： 是△重心

,

又∥,

,,

则.

（2）（1）中结论成立，理由如下：

如图，过点作∥交的延长线于点，、的延长线相交于点，

则，

又

而是的中点，即

又

结论成立；

（3）（1）中结论不成立，理由如下：

当点与点重合时，为中点，,

点在的延长线上时，,

,则，

同理：当点在的延长线上时，，

结论不成立.