Question

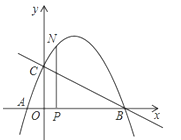
【题目】如图，抛物线与轴交于、两点，是以点（0,3）为圆心，2为半径的圆上的动点，是线段的中点，连结.则线段的最大值是（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

根据抛物线解析式可求得点A（-4,0），B（4,0），故O点为AB的中点，又Q是AP上的中点可知OQ=BP，故OQ最大即为BP最大，即连接BC并延长BC交圆于点P时BP最大，进而即可求得OQ的最大值.

∵抛物线与轴交于、两点

∴A（-4,0），B（4,0），即OA=4.

在直角三角形COB中

BC=

∵Q是AP上的中点，O是AB的中点

∴OQ为△ABP中位线，即OQ=BP

又∵P在圆C上，且半径为2，

∴当B、C、P共线时BP最大，即OQ最大

此时BP=BC+CP=7

OQ=BP=.