题目内容
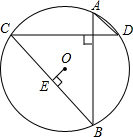 如图在⊙O中,AB⊥CD,OE⊥BC于E,则
如图在⊙O中,AB⊥CD,OE⊥BC于E,则| OE | AD |
分析:如图,连接CO并延长交⊙O于点F,连接BF,连接AC,设AB、CD交于点G,由圆周角定理可知∠F=∠CAB,由互余关系可知∠F+∠FCB=90°,∠CAB+∠ACD=90°,可得∠FCB=∠ACD,则BF=AD,由中位线定理可知BF=2OE,即AD=2OE.
解答: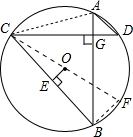 解:如图,连接CO并延长交⊙O于点F,连接BF,连接AC,设AB、CD交于点G,
解:如图,连接CO并延长交⊙O于点F,连接BF,连接AC,设AB、CD交于点G,
由圆周角定理可知∠F=∠CAB,
∵CF为直径,∴∠F+∠FCB=90°,
∵AB⊥CD,∴∠CAB+∠ACD=90°,
∴∠FCB=∠ACD,则BF=AD,
∵OE⊥BC,∴CE=BE,又CO=FO,
∴由中位线定理可知BF=2OE,即AD=2OE,
∴
=
.
故答案为:
.
 解:如图,连接CO并延长交⊙O于点F,连接BF,连接AC,设AB、CD交于点G,
解:如图,连接CO并延长交⊙O于点F,连接BF,连接AC,设AB、CD交于点G,由圆周角定理可知∠F=∠CAB,
∵CF为直径,∴∠F+∠FCB=90°,
∵AB⊥CD,∴∠CAB+∠ACD=90°,
∴∠FCB=∠ACD,则BF=AD,
∵OE⊥BC,∴CE=BE,又CO=FO,
∴由中位线定理可知BF=2OE,即AD=2OE,
∴
| OE |
| AD |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了圆周角定理,三角形中位线定理圆心角、弧、弦的关系.关键是利用辅助线作出与
相等的弧
.
 |
| AD |
 |
| BF |

练习册系列答案
相关题目
 11、如图在△ABC中,AB<AC,BC边的垂直平分线DE交BC于D,交AC于E,AB=6cm,AC=8cm,则△ABE的周长为( )
11、如图在△ABC中,AB<AC,BC边的垂直平分线DE交BC于D,交AC于E,AB=6cm,AC=8cm,则△ABE的周长为( ) 如图在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.
如图在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.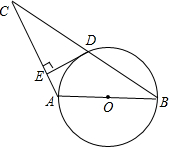 如图在△ABC中,AB=4,BC=
如图在△ABC中,AB=4,BC= (2014•宝山区一模)通过锐角三角比的学习,我们已经知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长比与角的大小之间可以相互转化.类似的我们可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图在△ABC中,AB=AC,
(2014•宝山区一模)通过锐角三角比的学习,我们已经知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长比与角的大小之间可以相互转化.类似的我们可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图在△ABC中,AB=AC, 如图在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求:
如图在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求: