题目内容
 (2014•宝山区一模)通过锐角三角比的学习,我们已经知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长比与角的大小之间可以相互转化.类似的我们可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图在△ABC中,AB=AC,
(2014•宝山区一模)通过锐角三角比的学习,我们已经知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长比与角的大小之间可以相互转化.类似的我们可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=
| 底边 |
| 腰 |
| BC |
| AB |
(1)sad60°=
1
1
;sad90°=| 2 |
| 2 |
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是
0<sadA<2
0<sadA<2
.(3)试求sad36°的值.
分析:(1)根据等腰三角形的性质,求出底角的度数,判断出三角形为等边三角形,再根据正对的定义解答进而得出sad90°的值;
(2)求出0度和180度时等腰三角形底和腰的比即可;
(3)作出等腰△ABC,构造等腰三角形BCD,根据正对的定义解答.
(2)求出0度和180度时等腰三角形底和腰的比即可;
(3)作出等腰△ABC,构造等腰三角形BCD,根据正对的定义解答.
解答:解:(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°=
=1.
根据正对定义,
当顶角为90°时,等腰三角形底角为45°,
则三角形为等腰直角三角形,
则sad90°=
=
故答案为:1,
.
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为:0<sadA<2.
(3)如图所示:已知:∠A=36°,AB=AC,BC=BD,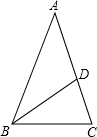
∴∠A=∠CBD=36°,∠ABC=∠C=72°,
∴△BCD∽△ABC,
∴
=
,
∴
=
,
解得:BC=
CD,
∴sad36°=
=
.
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°=
| 1 |
| 1 |
根据正对定义,
当顶角为90°时,等腰三角形底角为45°,
则三角形为等腰直角三角形,
则sad90°=
| ||
| 1 |
| 2 |
故答案为:1,
| 2 |
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为:0<sadA<2.
(3)如图所示:已知:∠A=36°,AB=AC,BC=BD,

∴∠A=∠CBD=36°,∠ABC=∠C=72°,
∴△BCD∽△ABC,
∴
| BC |
| AC |
| CD |
| BC |
∴
| BC |
| BC+CD |
| CD |
| BC |
解得:BC=
1+
| ||
| 2 |
∴sad36°=
| BC |
| CD |
1+
| ||
| 2 |
点评:本题考查了解直角三角形:利用三角函数的定义和相似三角形的判定与性质,根据题意得出BC与CD的关系是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2014•宝山区一模)已知Rt△ABC中,∠C=90°,那么cosA表示( )的值.
(2014•宝山区一模)已知Rt△ABC中,∠C=90°,那么cosA表示( )的值. (2014•宝山区一模)已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=
(2014•宝山区一模)已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE= (2014•宝山区一模)如图,梯形ABCD中,AD∥BC,BF⊥AD,CE⊥AD,且AF=EF=ED=5,BF=12,动点G从点A出发,沿折现AB-BC-CD以每秒1个单位长的速度运动到点D停止.设运动时间为t秒,△EFG的面积为y,则y关于t的函数图象大致是( )
(2014•宝山区一模)如图,梯形ABCD中,AD∥BC,BF⊥AD,CE⊥AD,且AF=EF=ED=5,BF=12,动点G从点A出发,沿折现AB-BC-CD以每秒1个单位长的速度运动到点D停止.设运动时间为t秒,△EFG的面积为y,则y关于t的函数图象大致是( )