题目内容
 如图在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求:
如图在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求:(1)AC的长度;
(2)△ABC的面积.
分析:(1)首先利用勾股定理逆定理证明∠ADB=90°,再利用勾股定理计算出AC的长即可;
(2)根据三角形的面积公式代入数计算即可.
(2)根据三角形的面积公式代入数计算即可.
解答:解:(1)∵AD是BC的中线,BC=10,
∴BD=CD=5,
∵52+122=132,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADC=90°,
∴AC=
=
=13;
(2)
×CB×AD=
×10×12=60.
∴BD=CD=5,
∵52+122=132,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADC=90°,
∴AC=
| AD2+CD2 |
| 144+25 |
(2)
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了勾股定理,以及勾股定理逆定理,根据题意证明∠ADC=90°是解决问题的关键.

练习册系列答案
相关题目

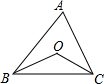 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE, 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是