Question

如图，P是⊙O外一点，PA切⊙O于A，AB是⊙O的直径，PB交⊙O于C，若PA=2cm，∠B=30°，求出图中阴影部分的面积．

Answer 1

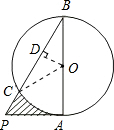解：连接CO，过O作OD⊥PB于点D，
∵∠B=30°，PA=2cm，
∴PB=4，AB=cm，
∴OB=OC=OA=cm，
∵∠B=30°，∴∠BOC=120°，∠AOC=60°，
∴OD=cm，BD=cm，BC=3cm，
∴S_△BOC=3××=cm²，S_扇形AOC==cm²，
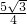∴S_阴影部分=×2×2--=-（cm²）．
分析：连接OC，可把空白部分分为扇形COA，△BOC，那么图中阴影部分面积=△PBA的面积-扇形COA的面积-△BOC．
点评：解决本题的关键是把所求的面积进行合理分割，分割为常见的容易算出的三角形，扇形．