题目内容
 如图,△ABC为⊙O的内接正三角形,P为弧BC上一点,PA交BC于D,已知PB=3,PC=6,则PD=
如图,△ABC为⊙O的内接正三角形,P为弧BC上一点,PA交BC于D,已知PB=3,PC=6,则PD=2
2
.分析:在PA上截取PE=PB,连接BE,则有△BEP是等边三角形,由SAS证得△ABE≌△CBP,则AE=CP,得到AP=AE+PE=PB+PC,即可求出AP的值,再证明△ABD∽△APB,得到BD和AB的数量关系,再证明△BPD∽△APC,即可求出PD的值.
解答: 解:在PA上截取PE=PB,连接BE;
解:在PA上截取PE=PB,连接BE;
∵△ABC是等边三角形,∠ACB=APB,
∴∠ACB=∠APB=60°,AB=BC;
∴△BEP是等边三角形,BE=PE=PB;
∴∠ACB-∠EBC=APB-∠EBC=60°-∠EBC;
∴∠ABE=∠CBP;
∵在△ABE与CBP中,
,
∴△ABE≌△CBP;
∴AE=CP;
∴AP=AE+PE=PB+PC.
∵PB=3,PC=6,
∴PA=6+3=9,
∵∠BAP=∠DAB(公共角),
∠ABC=∠ACB=∠APB=60°,
∴△ABD∽△APD,
∴
=
,
∴
=
,
∴BD=
AB=
AC,
∵∠PBD=∠PAC,
∠BPD=∠APC=60°,
∴△BPD∽△APC,
∴
=
,
∴
=
,
∴PD=6×
=2.
故答案为2.
 解:在PA上截取PE=PB,连接BE;
解:在PA上截取PE=PB,连接BE;∵△ABC是等边三角形,∠ACB=APB,
∴∠ACB=∠APB=60°,AB=BC;
∴△BEP是等边三角形,BE=PE=PB;
∴∠ACB-∠EBC=APB-∠EBC=60°-∠EBC;
∴∠ABE=∠CBP;
∵在△ABE与CBP中,
|
∴△ABE≌△CBP;
∴AE=CP;
∴AP=AE+PE=PB+PC.
∵PB=3,PC=6,
∴PA=6+3=9,
∵∠BAP=∠DAB(公共角),
∠ABC=∠ACB=∠APB=60°,
∴△ABD∽△APD,
∴
| AB |
| AP |
| BD |
| BP |
∴
| AB |
| 9 |
| BD |
| 3 |
∴BD=
| 1 |
| 3 |
| 1 |
| 3 |
∵∠PBD=∠PAC,
∠BPD=∠APC=60°,
∴△BPD∽△APC,
∴
| BP |
| AC |
| PD |
| PC |
∴
| ||
| AC |
| PD |
| 6 |
∴PD=6×
| 1 |
| 3 |
故答案为2.
点评:本题通过构造等边三角形,利用等边三角形的性质、全等三角形的判定和性质、求出某些线段的长度,再利用相似的判定定理和性质定理去求出未知线段的长度,综合性很强.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 种不同的平行四边形,并计算其中一种平行四边形的对角线的长.
种不同的平行四边形,并计算其中一种平行四边形的对角线的长. 5、如图,△ABC为⊙O的内接三角形,AB是直径,∠A=20°,则∠B的度数是( )
5、如图,△ABC为⊙O的内接三角形,AB是直径,∠A=20°,则∠B的度数是( )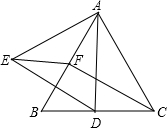 如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE. 22、如图,△ABC为等边三角形,又DE⊥BC,EF⊥AC,FD⊥AB,垂足分别为E,F,D,则△DEF是等边三角形吗?说明你的理由.
22、如图,△ABC为等边三角形,又DE⊥BC,EF⊥AC,FD⊥AB,垂足分别为E,F,D,则△DEF是等边三角形吗?说明你的理由.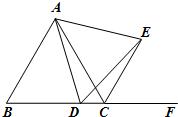 23、如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E.
23、如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E.