题目内容
如图，AB是⊙O的直径，AB=6，点C是AB延长线上一点，CD是⊙O的切线，点D是切点，过点B作⊙O的切线，交CD于点E，若BE=2，求CE的长．考点：切线的性质
专题：
分析：先根据切线的性质得出DE=BE=2，EB⊥AC，然后根据勾股定理求得BC，利用切割线定理，可求CE（负值不合题意，舍去）．
解答：解：∵CD是⊙O的切线，EB是⊙O的切线，
∴DE=BE=2，EB⊥AC，
∴BC=
=
，
由切割线定理，得
CD2=CB•CA，
CD2=CB（AB+CB），
（CE+2）2=
•（6+
）
整理得：5CE2-16CE-52=0，解得：CE=5.2；
∴CE的长为5.2．
∴DE=BE=2，EB⊥AC，
∴BC=
| EC2-BE2 |
| EC2-4 |
由切割线定理，得
CD2=CB•CA，
CD2=CB（AB+CB），
（CE+2）2=
| EC2-4 |
| EC2-4 |
整理得：5CE2-16CE-52=0，解得：CE=5.2；
∴CE的长为5.2．
点评：本题考查了切线的性质，切割线定理勾股定理的应用等，熟练掌握性质和定理是解题的关键．
练习册系列答案
相关题目
北宋末南宋初，中国象棋基本定型，开始风行全国．中国象棋规定：马走“日”（“
”）字．现定义：在中国象棋的棋盘上，如图，从点A到点B，马走的最小步数称为A与B的马步距离．记作|AB|m，在图中画出了中国象棋的一部分，上面标有A，B，C，D，E共5个点，则在|AB|m、|AC|m、|AD|m、|AE|m中哪个最大？哪个最小？
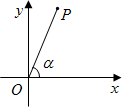如图，在直角坐标系中，P是第一象限内的点，其坐标是（4，m），且OP与x轴正半轴的夹角α的余弦值是| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|