题目内容
11.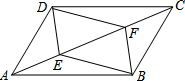 在平行四边形ABCD中,点E、F分别在对角线AC上,且AE=CF,连结DE、BE、DF、BF,则四边形DEBF是平行四边形吗?为什么?
在平行四边形ABCD中,点E、F分别在对角线AC上,且AE=CF,连结DE、BE、DF、BF,则四边形DEBF是平行四边形吗?为什么?
分析 先连接BD,交AC于O,由于四边形ABCD是平行四边形,易知OB=OD,OA=OC,而AE=CF,根据等式性质易得OE=OF,再根据两组对角线互相平分的四边形是平行四边形可证之.
解答  解:四边形DEBF是平行四边形
解:四边形DEBF是平行四边形
理由:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵AE=CF,
∴AE-AO=CF-OC,
∴OE=OF,
∴四边形DEBF是平行四边形(对角线互相平分的四边形是平行四边形).
点评 本题考查了平行四边形的判定和性质,解题的关键是作辅助线,使其中出现对角线相交的情况.

练习册系列答案
相关题目
19.计算3.8×10-7-3.7×10-7,结果用科学记数法表示为( )
| A. | 0.1×10-7 | B. | 1×10-6 | C. | 0.1×10-8 | D. | 1×10-8 |
16.方程3x-2y=7的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ |
3.将一元二次方程3x2-1=4x化成一般形式为( )
| A. | 3x2+4x=1 | B. | 3x2-4x=1 | C. | 3x2-4x-1=0 | D. | 3x2+4x-1=0 |
20.用配方法解下列方程,其中应在方程左、右两边同时加上4的是( )
| A. | x2-2x=5 | B. | 2x2-4x=5 | C. | x2+4x=5 | D. | 4x2+4x=5 |
1. 如图,直线l1∥l2,AB⊥CD,∠1=56°,则∠2等于( )
如图,直线l1∥l2,AB⊥CD,∠1=56°,则∠2等于( )
 如图,直线l1∥l2,AB⊥CD,∠1=56°,则∠2等于( )
如图,直线l1∥l2,AB⊥CD,∠1=56°,则∠2等于( )| A. | 56° | B. | 54° | C. | 44° | D. | 34° |