题目内容
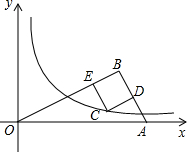 如图,在Rt△OAB中,∠B=Rt∠,OB=2AB.线段AB的垂直平分线交反比例函数y=
如图,在Rt△OAB中,∠B=Rt∠,OB=2AB.线段AB的垂直平分线交反比例函数y= (x>0)的图象于点C,D为垂足,过C作CE⊥OB于点E.当四边形CDBE为正方形时,正方形CDBE的面积为________.
(x>0)的图象于点C,D为垂足,过C作CE⊥OB于点E.当四边形CDBE为正方形时,正方形CDBE的面积为________.

分析:延长EC、DC,分别交x轴与P、F点,作CH⊥x轴于H点,设正方形CDBE的边长为a,根据垂直平分线的性质得AB=2a,则OB=2AB=4a,且可得到DF为△OAB的中位线,所以FD=
 OB=2a,则FC=2a-a=a,于是CP为△FDA的中位线,CP=
OB=2a,则FC=2a-a=a,于是CP为△FDA的中位线,CP= AD=
AD= a,在Rt△CFP中,根据勾股定理计算出PF=
a,在Rt△CFP中,根据勾股定理计算出PF= a,利用面积法计算出CH=
a,利用面积法计算出CH= a,在Rt△CFH中,根据勾股定理计算HF=
a,在Rt△CFH中,根据勾股定理计算HF= a,OA=2
a,OA=2 a,所以OF=
a,所以OF= OA=
OA= a,则可确定C点坐标为(
a,则可确定C点坐标为(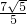 a,
a, a),然后把C点坐标代入反比例解析式得到a2.
a),然后把C点坐标代入反比例解析式得到a2.解答:延长EC、DC,分别交x轴与P、F点,作CH⊥x轴于H点,如图,
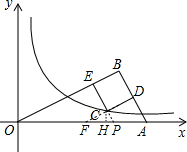
设正方形CDBE的边长为a,
∵FD垂直平分AB,
∴AB=2a,
∵OB=2AB,
∴OB=4a,
∵DF为△OAB的中位线,
∴FD=
 OB=2a,
OB=2a,∴FC=2a-a=a,
∴CP为△FDA的中位线,
∴CP=
 AD=
AD= a,
a,在Rt△CFP中,PF=
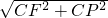 =
= a,
a,∴
 CH•PF=
CH•PF= CP•CF,即
CP•CF,即 CH•
CH• a=
a= a•
a• a,
a,∴CH=
 a,
a,在Rt△CFH中,HF=
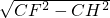 =
= a,
a,在Rt△OAB中,OA=
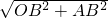 =2
=2 a,
a,∴OF=
 OA=
OA= a,
a,∴OH=OF+FH=
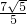 a,
a,∴C点坐标为(
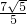 a,
a, a),
a),把C(
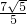 a,
a, a)代入y=
a)代入y= 得
得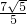 a•
a• a=2,解得a2=
a=2,解得a2= .
.∴正方形CDBE的面积为
 .
.点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和正方形的性质;熟练运用勾股定理进行几何计算.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
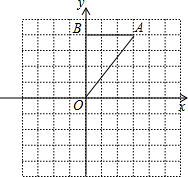 如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).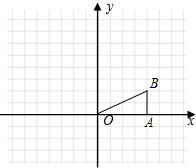 OA1B1.
OA1B1.
 如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1. (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.