题目内容
如图，在Rt△OAB中，∠OAB=90°，且点B的坐标为（4，2），将△OAB绕点O逆时针旋转90°后得△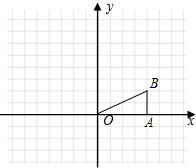
OA1B1．（1）在图中作出△OA1B1并直接写出A1，B1的坐标；
（2）求点B旋转到点B1所经过的路线长（结果保留π）．
分析：（1）首先作出旋转后的图形，即可确定点的坐标；
（2）旋转的路线是弧，利用弧长的计算公式即可求解．
（2）旋转的路线是弧，利用弧长的计算公式即可求解．
解答：
（本题满分6分）
解：（1）作出△OA1B1，如图（1分）A1（0，4），B1（-2，4）；（2分）
（2）∵OA=4，AB=2，
∴OB=2
，（1分）
∴l
=
=
π．（2分）
（本题满分6分）解：（1）作出△OA1B1，如图（1分）A1（0，4），B1（-2，4）；（2分）
（2）∵OA=4，AB=2，
∴OB=2
| 5 |
∴l
 |
| BB1 |
90×π×2
| ||
| 180 |
| 5 |
点评：本题主要考查了图形的旋转的作图以及弧长的计算公式，正确确定旋转角是解题的关键．
练习册系列答案
相关题目
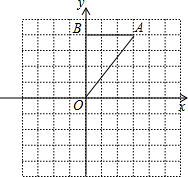如图，在Rt△OAB中，∠OBA=90°，且点B的坐标为（0，4）．
如图，在Rt△OAB中，∠OBA=90°，OB=AB=4，将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1．
（2009•株洲）如图，在Rt△OAB中，∠OAB=90°，OA=AB=6，将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1．