��Ŀ����
 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��һ�κ���y=
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��һ�κ���y=
| ||
| 3 |
��1���������ߵĽ���ʽ��
��2������DC��AC���������������ҳ���P��ʹ��7S��ACD=S��PAD��
��3��ֱ��y=
| ||
| 3 |
| ||
| 3 |
���㣺���κ����ۺ���
ר�⣺̽����
��������1������������y=ax2+bx+c����A��0��3�����������ߵĶ�������ΪC��1��4���г�����a��b��c�ķ����飬���a��b��c��ֵ���ɵó������ߵĽ���ʽ��
��2���ȸ��������ߵĶ�������Ϊ��1��4�����ʿɵó�D�����꣬���������ߵĶ�������Ϊ��1��4��������P�����x����·�����P������Ϊ��x��-x2+2x+3������-x2+2x+3��0���ٸ���7S��ACD=S��PAD���x��ֵ���ɣ�
��3���ѵ�A��0��3������ֱ��y=
x+m���m��ֵ���ʿɵó�ֱ�ߵĽ���ʽ������B����x��ĶԳƵ�B�䣬����B����ֱ��y=
x+m�Ĵ��߽�ֱ��AD�ڵ�E�����ݻ��ഹֱ������ֱ��б�ʵĻ�����1���ֱ��B��E�Ľ���ʽ���ʿɵó�E�����꣮
��2���ȸ��������ߵĶ�������Ϊ��1��4�����ʿɵó�D�����꣬���������ߵĶ�������Ϊ��1��4��������P�����x����·�����P������Ϊ��x��-x2+2x+3������-x2+2x+3��0���ٸ���7S��ACD=S��PAD���x��ֵ���ɣ�
��3���ѵ�A��0��3������ֱ��y=
| ||
| 3 |
| ||
| 3 |
����⣺��1����������y=ax2+bx+c����A��0��3�����������ߵĶ�������ΪC��1��4����
���
��
��������ߵĽ���ʽΪ��y=-x2+2x+3��
��2����ͼ1��
��A��0��3����C��1��4����AD��x�ᣬ
��D��2��3����
��CF=1��
��P��x��-x2+2x+3����
�ߵ�C�������ߵĶ������꣬
���P����x���·���
�ߡ�ACD���PADͬ�ף�7S��ACD=S��PAD��
��-��-x2+2x+3��=7-3=4�����x=1��2
��
��P��1+2
��-4����1-2
��-4����
��3���ߵ�A��0��3����ֱ��y=
x+m�ϣ�
��m=3��
��ֱ��y=
x+m�Ľ���ʽΪy=
x+3��
��C��1��4����
��ֱ��CF�Ľ���ʽΪx=1��
��B��1��
+3����
��ͼ2������B����AD�ĶԳƵ�B�䣬����B����ֱ��y=
x+m�Ĵ��߽�ֱ��AD�ڵ�E����E �㼴Ϊ����
�㼴Ϊ����
��ֱ��B��E��AB��
����ֱ��B��E�Ľ���ʽΪy=-
x+b��
�ߵ�B���B�����ֱ��AD�Գƣ�AD��x�ᣬAD�Ľ���ʽΪy=3��
��B�䣨1��3-
����
��3-
=-
+b�����b=3+
��
��ֱ��B��E�Ľ���ʽΪy=-
x+3+
��
�൱y=3ʱ��x=
��
��E��
��3����
���
|
��������ߵĽ���ʽΪ��y=-x2+2x+3��
��2����ͼ1��

��A��0��3����C��1��4����AD��x�ᣬ
��D��2��3����
��CF=1��
��P��x��-x2+2x+3����
�ߵ�C�������ߵĶ������꣬
���P����x���·���
�ߡ�ACD���PADͬ�ף�7S��ACD=S��PAD��
��-��-x2+2x+3��=7-3=4�����x=1��2
| 2 |
��P��1+2
| 2 |
| 2 |
��3���ߵ�A��0��3����ֱ��y=
| ||
| 3 |
��m=3��
��ֱ��y=
| ||
| 3 |
| ||
| 3 |
��C��1��4����
��ֱ��CF�Ľ���ʽΪx=1��
��B��1��
| ||
| 3 |
��ͼ2������B����AD�ĶԳƵ�B�䣬����B����ֱ��y=
| ||
| 3 |
 �㼴Ϊ����
�㼴Ϊ������ֱ��B��E��AB��
����ֱ��B��E�Ľ���ʽΪy=-
| 3 |
�ߵ�B���B�����ֱ��AD�Գƣ�AD��x�ᣬAD�Ľ���ʽΪy=3��
��B�䣨1��3-
| ||
| 3 |
��3-
| ||
| 3 |
| 3 |
2
| ||
| 3 |
��ֱ��B��E�Ľ���ʽΪy=-
| 3 |
2
| ||
| 3 |
�൱y=3ʱ��x=
| 2 |
| 3 |
��E��
| 2 |
| 3 |
���������⿼����Ƕ��κ����ۺ��⣬��֪�ô���ϵ������һ�κ��������κ����Ľ���ʽ�ǽ�����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼֱ������������ǵĽ�ƽ���������ɵĽǵĶ����ǣ�������
��ͼֱ������������ǵĽ�ƽ���������ɵĽǵĶ����ǣ�������| A��115�� | B��135�� |
| C��120�� | D�������� |
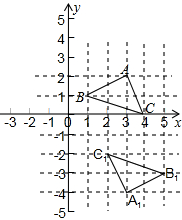 ��ͼ����ƽ��ֱ������ϵ�У�����BAC���A1B1C1���ڵ�E�����ĶԳƣ���Գ����ĵ�E�������ǣ�������
��ͼ����ƽ��ֱ������ϵ�У�����BAC���A1B1C1���ڵ�E�����ĶԳƣ���Գ����ĵ�E�������ǣ�������| A����2��-1�� |
| B����3��-1�� |
| C����4��-1�� |
| D����3��-2�� |
 ��ͼ����ͷ���һ�룬��ͼ������Ϊ�Գ��ử��������һ�룮
��ͼ����ͷ���һ�룬��ͼ������Ϊ�Գ��ử��������һ�룮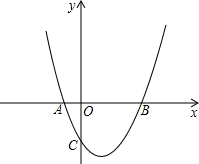 ��ͼ��������y=x2+bx+c��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C��
��ͼ��������y=x2+bx+c��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C�� ��ͼ����֪���κ���y=ax2+bx+c��ͼ����A��3��0����B��2��-3����C��0��-3����
��ͼ����֪���κ���y=ax2+bx+c��ͼ����A��3��0����B��2��-3����C��0��-3���� ��ͼ����ABC�У���֪BE��AD��CF��AD����BE=CF��
��ͼ����ABC�У���֪BE��AD��CF��AD����BE=CF��