题目内容
 如图,△ABC中,已知BE⊥AD,CF⊥AD,且BE=CF.
如图,△ABC中,已知BE⊥AD,CF⊥AD,且BE=CF.(1)证明:△BDE≌△CDF;
(2)给△ABC添加一个条件
(直接填写添加的条件,不需要证明.)
考点:全等三角形的判定与性质
专题:
分析:(1)求出∠BED=∠CFD=90°,根据AAS推出三角形全等即可;
(2)根据全等三角形性质得出BD=DC,根据等腰三角形的性质进行推出答案.
(2)根据全等三角形性质得出BD=DC,根据等腰三角形的性质进行推出答案.
解答:(1)证明:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BDE和△CDF中
,
∴△BDE≌△CDF(AAS);
(2)解:AB=AC,理由是:
∵△BDE≌△CDF,
∴BD=DC,
∵AB=AC,
∴AD平分∠BAC,
故答案为:AB=AC.
∴∠BED=∠CFD=90°.
在△BDE和△CDF中
|
∴△BDE≌△CDF(AAS);
(2)解:AB=AC,理由是:
∵△BDE≌△CDF,
∴BD=DC,
∵AB=AC,
∴AD平分∠BAC,
故答案为:AB=AC.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质的应用,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,抛物线y=ax2+bx+c与一次函数
如图,在平面直角坐标系中,抛物线y=ax2+bx+c与一次函数 如图,已知∠1=34°40′,OD平分∠BOC,求∠AOD的度数.
如图,已知∠1=34°40′,OD平分∠BOC,求∠AOD的度数. 如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,DG∥BC,求正方形DEFG面积的最大值.
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,DG∥BC,求正方形DEFG面积的最大值.
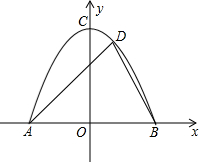 某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-
某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-