题目内容
11.如果a,b是一元二次方程x2-2x-4=0的两个根,那么a3b-2a2b的值为( )| A. | -8 | B. | 8 | C. | -16 | D. | 16 |
分析 先根据根与系数的关系得到ab=-4,再把原式表示得到原式=a2•ab-2a•ab,利用整体代入的方法可化简得到原式=-4a2+8a,接着根据一元二次方程解的定义得到a2=2a+4,然后再次利用整体代入的方法计算即可.
解答 解:根据题意,ab=-4,
所以原式=a2•ab-2a•ab
=-4a2-2a•(-4)
=-4a2+8a,
∵a是一元二次方程x2-2x-4=0的根,
∴a2-2a-4=0,即a2=2a+4,
∴原式=-4(2a+4)+8a
=-8a-16+8a
=-16.
故选C.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了一元二次方程的定义.

练习册系列答案
相关题目
1.在下列实数中,无理数是( )
| A. | π | B. | -$\frac{22}{7}$ | C. | $\sqrt{9}$ | D. | 0.1010010001 |
20.下列命题中正确的是( )
①三边对应成比例的两个三角形相似
②二边对应成比例且一个角对应相等的两个三角形相似
③一个锐角对应相等的两个直角三角形相似
④一个角对应相等的两个等腰三角形相似.
①三边对应成比例的两个三角形相似
②二边对应成比例且一个角对应相等的两个三角形相似
③一个锐角对应相等的两个直角三角形相似
④一个角对应相等的两个等腰三角形相似.
| A. | ①③ | B. | ①④ | C. | ①②④ | D. | ①③④ |
1.在下列四个一元二次方程中,没有实数根的一个是( )
| A. | x2-8x+1=0 | B. | 2x2+1=3x | C. | 3x2-6x+4=0 | D. | (x-2)2-1=0 |
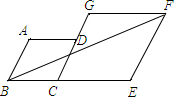 如图,在菱形ABCD和菱形CEFG中,B、C、E三点在一条直线上,C、D、G三点在一条直线上,若菱形ABCD边长为3,则当菱形CEFG的边长为$\frac{3+3\sqrt{5}}{2}$时,AG∥BF.
如图,在菱形ABCD和菱形CEFG中,B、C、E三点在一条直线上,C、D、G三点在一条直线上,若菱形ABCD边长为3,则当菱形CEFG的边长为$\frac{3+3\sqrt{5}}{2}$时,AG∥BF.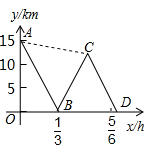 “五一”小长假,小明和妈妈准备乘动车去北京旅游,离火车出发还有一个小时.小明的爸爸骑摩托车想尽快将小明和妈妈俩从家送到汉口火车站.由于摩托车后座只能坐1人,为了节约时间,爸爸骑摩托车先带着小明出发,同时,小明的妈妈也步行出发沿同一路线去火车站.已知小明妈妈步行的速度是5km/h,摩托车的速度是45km/h.爸爸将小明送到车站后,立即回去接妈妈,再将妈妈送到车站.图中折线A-B-C-D、线段AC分别表示爸爸、妈妈在上述过程中,离车站的路程y(km)与爸爸所用时间x(h)之间的函数关系.根据图中的信息可知:当妈妈到达火车站时离火车开车的时间还有10分钟.
“五一”小长假,小明和妈妈准备乘动车去北京旅游,离火车出发还有一个小时.小明的爸爸骑摩托车想尽快将小明和妈妈俩从家送到汉口火车站.由于摩托车后座只能坐1人,为了节约时间,爸爸骑摩托车先带着小明出发,同时,小明的妈妈也步行出发沿同一路线去火车站.已知小明妈妈步行的速度是5km/h,摩托车的速度是45km/h.爸爸将小明送到车站后,立即回去接妈妈,再将妈妈送到车站.图中折线A-B-C-D、线段AC分别表示爸爸、妈妈在上述过程中,离车站的路程y(km)与爸爸所用时间x(h)之间的函数关系.根据图中的信息可知:当妈妈到达火车站时离火车开车的时间还有10分钟.