题目内容
11.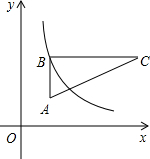 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC,BA分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,BC=4.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC,BA分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,BC=4.(1)求点C的坐标和AC所在的直线的解析式.
(2)若反比例函数y=$\frac{m}{x}$(x>0)的图象经过点B,求m是值;
(3)若反比例函数y=$\frac{m}{x}$(x>0)的图象与AC边有公共点,请直接写出m的取值范围.
分析 (1)利用待定系数法求直线AC的解析式;
(2)利用BC平行于x轴可确定B点坐标为(1,3),然后把B点坐标代入y=$\frac{m}{x}$即可计算出m的值;
(3)当反比例函数图象经过点C时,m最大;当反比例函数图象经过点A时,m最小.
解答 解:(1)∵两条直角边BC,BA分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,BC=4,
∴B点坐标为(1,3),点C的坐标为(5,3),
设直线AC的解析式为y=kx+b,把A(1,1)、C(5,3)代入得
$\left\{\begin{array}{l}{k+b=1}\\{5k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$.
∴直线AC的解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$;
(2)把B(1,3)代入y=$\frac{m}{x}$得m=1×3=3;
(3)当反比例函数图形经过点C(5,3),则m=5×3=15;
当反比例函数图形经过点A(1,1),则m=1×1=1,
所以m的取值范围为1≤m≤15.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
2.地球与太阳的距离约为150000000千米;将数字150000000用科学记数法表示为( )
| A. | 15×107千米 | B. | 1.5千米 | C. | 1.5×108千米 | D. | 0.15×107千米 |
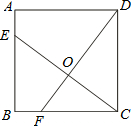 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD=$\frac{4}{3}$,④S△ODC=S四边形BEOF中,正确的有①③④.
如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD=$\frac{4}{3}$,④S△ODC=S四边形BEOF中,正确的有①③④.