题目内容
【题目】如图1,已知![]() 中,点
中,点![]() 在
在![]() 边上,
边上,![]() 交边
交边![]() 于点
于点![]() ,且
,且![]() 平分
平分![]() .
.
(1)求证:![]() ;
;
(2)如图2,在![]() 边上取点
边上取点![]() ,使
,使![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长。
的长。
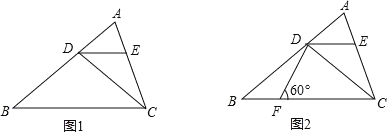
【答案】(1)见解析;(2)DF=3.
【解析】
(1)如图,根据平行线的性质可得∠1=∠B,∠2=∠3,根据角平分线的定义可得∠1=∠2,等量代换得到∠B=∠3,即可证明DB=DC;
(2)作DG⊥BC于点G,易求GB、GF的长,再根据在直角三角形中30°的锐角所对的直角边是斜边的一半即可求出DF的长.
解:(1)如图,∵DE∥BC,
∴∠1=∠B,∠2=∠3,
∵DE平分∠ADC,
∴∠1=∠2,
∴∠B=∠3,
∴DB=DC;
(2)作DG⊥BC于点G,
∵DB=DC,DG⊥BC,
∴GB=![]() BC=
BC=![]() ×7=3.5,
×7=3.5,
∴GF=GBBF=3.52=1.5,
∵Rt△DGF中,∠DFG=60°,
∴∠FDG=30°,
∴DF=2GF=2×1.5=3.


练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目