题目内容
【题目】如图，O是
的内心，BO的延长线和的外接圆相交于D，连结DC、DA、OA、OC，四边形OADC为平行四边形．
求证：
≌
．
若
，求阴影部分的面积．
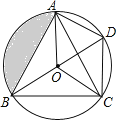
【答案】（1）证明见解析（2）
【解析】
由点O为三角形的内心，得到BO与CO都为角平分线，再由四边形AOCD为平行四边形，得到对边平行且相等，进而利用AAS得到三角形全等；
由三角形全等得到对应边相等，对应角相等，确定出三角形ABC为等边三角形，可得出内心与外心重合，即
，阴影部分面积等于扇形AOB面积减去三角形AOB面积，求出即可．
是
的内心，
，
，
，
，
由
，
，
，
在
和
中，
，
≌
；
由得，
，
，
，
，
是等边三角形，
是的内心也是外心，
，
设E为BD与AC的交点，BE垂直平分AC，
在
中，
，
，
，
，
．
练习册系列答案
相关题目
【题目】某商场分两次购进A，B两种商品进行销售，两次购进同一种商品的进价相同，具体情况如表所示：
购进数量 | 购进所需费用 | ||
A | B | ||
第一次 | 30 | 20 | 2200 |
第二次 | 20 | 30 | 2800 |
求A，B两种商品每件的进价分别是多少元？
商场决定A种商品以每件30元出售，B种商品以每件100元出售
为满足”五一“小长假期间市场需求，需购进A，B两种商品共1000件，且A种商品的数量不少于B种商品数量的4倍，请你求出获利最大的进货方案，此时最大利润是多少？
