��Ŀ����
����Ŀ�����Ķ���




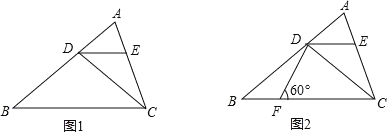
��ͼ����A������DM�ϵ�һ�����㣬��ADΪ�����ı���ABCD����![]() ��
��![]() ��
��![]() ��
��![]() ��ֱ��l������D�������ı��εı�BC��BA�ཻ����ֱ��l��DC�ļн�
��ֱ��l������D�������ı��εı�BC��BA�ཻ����ֱ��l��DC�ļн�![]() �����ı���ABCD��ֱ��
�����ı���ABCD��ֱ��![]() ��ֱ��l�۵�����C���ڵ�
��ֱ��l�۵�����C���ڵ�![]() ������B���ڵ�
������B���ڵ�![]() ��
��![]() ��AD�ij�Ϊm��
��AD�ij�Ϊm��
�����⣩
����![]() ���A�غ�
���A�غ�![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() ��
��
�����ԣ�
![]() ��
��![]() ʱ������
ʱ������![]() ���ı���ABCD�ı�AB��
���ı���ABCD�ı�AB��![]() ��ͼ
��ͼ![]() ����m��ֵ��
����m��ֵ��
![]() ����
����![]() ǡΪAB���е�
ǡΪAB���е�![]() ��ͼ
��ͼ![]() ����
����![]() �Ķ�����
�Ķ�����
��̽����
![]() ��ֱ��
��ֱ��![]() ����ֱ��AD���ڵ�G����ֱ��AB���ڵ�H����
����ֱ��AD���ڵ�G����ֱ��AB���ڵ�H����![]() ��
��![]() ��һ�����Ƶĵ���������ʱ����ֱ��д��
��һ�����Ƶĵ���������ʱ����ֱ��д��![]() �����Ӧ��mֵ��
�����Ӧ��mֵ��
���𰸡���1��5����2��30�㣻��3��![]() ��
��![]() ��
��
��������
![]() ���
���![]() ��
��![]() ���ɽ�����⣻
���ɽ�����⣻
![]() ���ͼ1��ʾ������C
���ͼ1��ʾ������C![]() ���ӳ�����AD�ڵ�
���ӳ�����AD�ڵ�![]() ֻҪ֤��
ֻҪ֤��![]() ��
��![]() ��
��![]() Ϊ�ȱ������μ��ɽ�����⣻
Ϊ�ȱ������μ��ɽ�����⣻
![]() ���������ηֱ�ͼ�Σ����ɽ�����⣻
���������ηֱ�ͼ�Σ����ɽ�����⣻
![]() ��B���ڵ�B1�������C1����DM�ϣ�
��B���ڵ�B1�������C1����DM�ϣ�![]() ֱ��l�����ͼ2��ʾ��
ֱ��l�����ͼ2��ʾ��

���۵���֪��![]() ��
��![]() ��
��
![]() ֱ��l��
ֱ��l��![]() ��
��
![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
![]() ��
��
![]() ��
��
![]() ��
��
![]() ���ͼ1��ʾ������C
���ͼ1��ʾ������C![]() ���ӳ�����AD�ڵ�F��
���ӳ�����AD�ڵ�F��

��![]() ��
��![]() ��
�У�
 ��
��
![]() ��
��![]() ��
��
![]() ������
������![]() Ϊ
Ϊ![]() б��CF���е㣬
б��CF���е㣬
![]() ��
��
�����۵���֪��![]() ��
��
![]() ��
��
![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() ��
��
![]() ��
��
![]() ��ͼ3�У���
��ͼ3�У���![]() ��
��![]() ��
��![]() ��
��![]() ʱ��
ʱ��
��֤![]() ���ɵ�
���ɵ�![]() ��
��
![]() ��
��
![]() �ǵȱ������Σ�
�ǵȱ������Σ�
![]() ����
����![]() ��K��
��K��

���ı���DCBK�Ǿ��Σ�![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��ͼ4�У���
��ͼ4�У���![]() ��
��![]() ��
��![]() ��
��![]() ʱ��ͬ���ɵ�
ʱ��ͬ���ɵ�![]() ��
��![]() ��
��

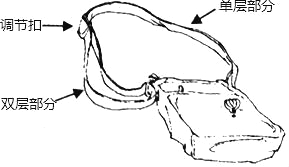
����Ŀ����ͼ����һ��б�����������˫�㲿�֡����㲿�ֺ͵��ڿ۹��ɣ�С���ú��֣�ͨ�����ڿۼӳ������̵��㲿�ֵij��ȣ�����ʹ����ij��ȣ����㲿����˫�㲿�ֳ��ȵĺͣ����е��ڿ���ռ�ij��Ⱥ��Բ��ƣ��ӳ������̣��赥�㲿�ֵij���Ϊxcm��˫�㲿�ֵij���Ϊycm�����������õ��������ݣ�
���㲿�ֵij���x��cm�� | �� | 4 | 6 | 8 | 10 | �� | 150 |
˫�㲿�ֵij���y��cm�� | �� | 73 | 72 | 71 | �� |
��1�����ݱ������ݵĹ��ɣ�������±���ֱ��д��y����x�ĺ�������ʽ��
��2������С�������ߺ�ϰ�ߣ�����ij���Ϊ120cmʱ�������������ʣ��������ʱ���㲿�ֵij��ȣ�
��3�������ij���Ϊlcm����l��ȡֵ��Χ��