题目内容
如图，BD是等腰△ABC底角平分线，若底角∠ABC=72°，腰AB长4cm，则底BC长为________cm．
（-2+2
）
分析：等腰三角形的底角相等，因为BD是等腰△ABC底角平分线，所以∠DBC可求出，∠ABD也可求出，从而可看出BC=BD=AD，然后设BC=x，则AD=BD=BC=x，DC=4-x，利用相似关系求出x．
解答：∵BD是等腰△ABC底角平分线，若底角∠ABC=72°，
∴∠A=36°，∠C=72°，∠ABD=∠CBD=36°，
∴∠BDC=72°，
∴BD=BC=AD，
设BC=x，则AD=BD=BC=x，DC=4-x，
∵△BCD∽△ABC，
∴
=
x=-2+2或x=-2-2（舍去）．
故答案为：（-2+2）．
点评：本题考查等腰三角形的性质，底角相等，等角对等边，以及相似三角形的对应边成比例．
）分析：等腰三角形的底角相等，因为BD是等腰△ABC底角平分线，所以∠DBC可求出，∠ABD也可求出，从而可看出BC=BD=AD，然后设BC=x，则AD=BD=BC=x，DC=4-x，利用相似关系求出x．
解答：∵BD是等腰△ABC底角平分线，若底角∠ABC=72°，
∴∠A=36°，∠C=72°，∠ABD=∠CBD=36°，
∴∠BDC=72°，
∴BD=BC=AD，
设BC=x，则AD=BD=BC=x，DC=4-x，
∵△BCD∽△ABC，
∴
=x=-2+2
或x=-2-2（舍去）．故答案为：（-2+2
）．点评：本题考查等腰三角形的性质，底角相等，等角对等边，以及相似三角形的对应边成比例．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
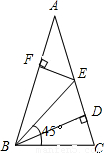
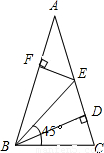
7、如图，BD是等腰△ABC（顶角∠A是锐角）腰AC上的高，在△ABC内作一只45°的角∠EBC交AC于点E，过E作AB的垂线段EF，垂足为F．则线段DE与线段EF的大小关系为（ ）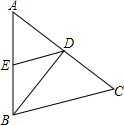
如图，BD是等腰三角形ABC的底边AC上的高线，DE∥BC，交AB于点E．则△BDE是等腰三角形．请在解答过程中的括号里填写理由．
