题目内容
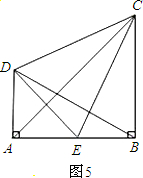
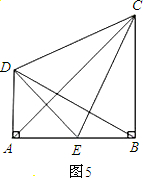
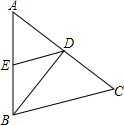如图，BD是等腰三角形ABC的底边AC上的高线，DE∥BC，交AB于点E．则△BDE是等腰三角形．请在解答过程中的括号里填写理由．解：∵AB=BC，BD⊥AC（已知）∴∠ABD=∠DBC
（三线合一）
（三线合一）
∵DE∥BC（已知），∴∠DBC=∠EDB，
（两直线平行，内错角相等）
（两直线平行，内错角相等）
∴∠ABD=∠EDB，∴BE=DE
（等角对等边）
（等角对等边）
∴△EDB是等腰三角形．
分析：由AB=BC，BD⊥AC（已知）得到∠ABD=∠DBC，是根据三线合一的性质证得的；由DE∥BC（已知），得到∠DBC=∠EDB，是根据平行线的性质得到的，由等角对等边，可由∠ABD=∠EDB，证得BE=DE．
解答：解：∵AB=BC，BD⊥AC（已知），
∴∠ABD=∠DBC （三线合一），
∵DE∥BC（已知），
∴∠DBC=∠EDB，（两直线平行，内错角相等）
∴∠ABD=∠EDB，
∴BE=DE （等角对等边）
∴△EDB是等腰三角形．
故答案为：（三线合一），（两直线平行，内错角相等），（等角对等边）．
∴∠ABD=∠DBC （三线合一），
∵DE∥BC（已知），
∴∠DBC=∠EDB，（两直线平行，内错角相等）
∴∠ABD=∠EDB，
∴BE=DE （等角对等边）
∴△EDB是等腰三角形．
故答案为：（三线合一），（两直线平行，内错角相等），（等角对等边）．
点评：此题考查了等腰三角形的性质与判定以及平行线的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
