题目内容
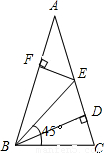
如图,BD是等腰△ABC(顶角∠A是锐角)腰AC上的高,在△ABC内作一只45°的角∠EBC交AC于点E,过E作AB的垂线段EF,垂足为F.则线段DE与线段EF的大小关系为( )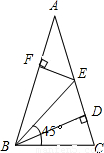
A.DE>EF
B.DE=EF
C.DE<EF
D.与∠A的大小有关,无法判断
【答案】分析:先根据△ABC是等腰三角形和∠EBC=45度,求出∠FBE=∠DBE,然后得到△BEF≌△BED,从而求出DE=EF.
解答:解:设∠DBC=y度,∠FBE=x度,则∠C=∠ABC=(45+x)度.
在△CBD中,y+45+x=90,
即x=45-y,
又∵∠EBD=45-y,
∴∠EBD=x度,
∴∠FBE=∠DBE,
在△BFE和△BDE中,
∠BFE=∠BDE,∠FBE=∠DBE,BE=BE,
∴△BFE≌△BDE,
∴DE=EF.
点评:此题考查等腰三角形的性质和全等三角形的性质与判定,设出未知角通过直角三角形锐角互补建立起各相关角之间的关系是解题的关键.
解答:解:设∠DBC=y度,∠FBE=x度,则∠C=∠ABC=(45+x)度.
在△CBD中,y+45+x=90,
即x=45-y,
又∵∠EBD=45-y,
∴∠EBD=x度,
∴∠FBE=∠DBE,
在△BFE和△BDE中,
∠BFE=∠BDE,∠FBE=∠DBE,BE=BE,
∴△BFE≌△BDE,
∴DE=EF.
点评:此题考查等腰三角形的性质和全等三角形的性质与判定,设出未知角通过直角三角形锐角互补建立起各相关角之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 7、如图,BD是等腰△ABC(顶角∠A是锐角)腰AC上的高,在△ABC内作一只45°的角∠EBC交AC于点E,过E作AB的垂线段EF,垂足为F.则线段DE与线段EF的大小关系为( )
7、如图,BD是等腰△ABC(顶角∠A是锐角)腰AC上的高,在△ABC内作一只45°的角∠EBC交AC于点E,过E作AB的垂线段EF,垂足为F.则线段DE与线段EF的大小关系为( )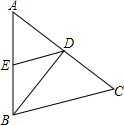 如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.则△BDE是等腰三角形.请在解答过程中的括号里填写理由.
如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.则△BDE是等腰三角形.请在解答过程中的括号里填写理由.