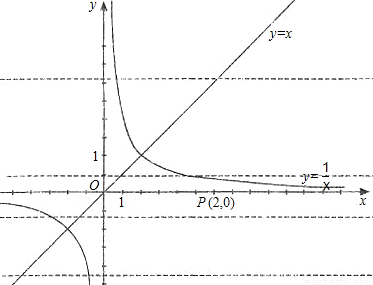
题目内容
已知：ab=1且a=2-| 3 |
分析：（1）根据ab=1，变形后用a表示出b，把a的值代入，分子分母同时乘以分母的有理化因式2+
，分母利用平方差公式计算，即可得到b的值；
（2）由（1）中求出的b值，以及已知的a值，代入所求的式子中，去括号抵消后，根据乘方的意义即可得出最后结果．
| 3 |
（2）由（1）中求出的b值，以及已知的a值，代入所求的式子中，去括号抵消后，根据乘方的意义即可得出最后结果．
解答：解：（1）∵ab=1且a=2-
，
∴b=
=
=
=
=2+
；
（2）由a=2-
与（1）中求出的b=2+
，
代入得：(a-b)2=[(2-
)-(2+
)]2
=(2-
-2-
)2=(-2
)2
=12．
| 3 |
∴b=
| 1 |
| a |
| 1 | ||
2-
|
2+
| ||||
(2-
|
2+
| ||
22-(
|
| 3 |
（2）由a=2-
| 3 |
| 3 |
代入得：(a-b)2=[(2-
| 3 |
| 3 |
=(2-
| 3 |
| 3 |
| 3 |
=12．
点评：此题考查了二次根式的化简求值，在进行二次根式的化简时，若分母中含有根号，化简的方法是找出分母的有理化因式，根据分数的基本性质分子分母都乘以有理化因式，从而达到化简的目的，且无论是计算还是化简，最后结果必须是最简．
练习册系列答案
相关题目
如图，已知：AB=DE且AB∥DE，BE=CF．求证：∠A=∠D．
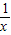的图象分别交于点A和点B，又有定点P（2，0）．
，求线段AB的长；
，且在它的对称轴左边时，y随着x的增大而增大，试求出满足条件的抛物线的解析式；
x2的图象，求点P到直线AB的距离．