题目内容
3．计算（1）100$\frac{1}{40}$×（-20）
（2）-|-5|+（-3）3÷（-22）
（3）60÷（-$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{5}$）
（4）9-（${\frac{1}{2}$+$\frac{2}{3}$-$\frac{3}{4}$-$\frac{11}{12}$）×（-24）
（5）-（-3）2-[3+0.4×（${-1\frac{1}{2}}$）]÷（-2）
（6）-14÷（-5）2×（-$\frac{5}{3}$）+|0.8-1|．
分析 （1）原式变形后，利用乘法分配律计算即可得到结果；
（2）原式先计算乘方运算，再计算除法运算，最后算加减运算即可得到结果；
（3）原式先计算括号中的运算，再计算除法运算即可得到结果；
（4）原式利用乘法分配律计算即可得到结果；
（5）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果；
（6）原式先计算乘方及绝对值运算，再计算乘除运算，最后算加减运算即可得到结果．
解答 解：（1）原式=（100+$\frac{1}{40}$）×（-20）=-2000-$\frac{1}{2}$=-2000$\frac{1}{2}$；
（2）原式=-5-27×（-$\frac{1}{4}$）=-5+$\frac{27}{4}$=$\frac{7}{4}$；
（3）原式=60÷（-$\frac{15}{30}$+$\frac{10}{30}$+$\frac{6}{30}$）=60÷$\frac{1}{30}$=60×30=1800；
（4）原式=9+12+16-18-22=-3；
（5）原式=-9-（3-$\frac{2}{5}$×$\frac{3}{2}$）×（-$\frac{1}{2}$）=-9+$\frac{3}{2}$-$\frac{3}{10}$=-10$\frac{1}{5}$；
（6）原式=-1×$\frac{1}{25}$×（-$\frac{5}{3}$）+0.2=$\frac{1}{15}$+$\frac{1}{5}$=$\frac{4}{15}$．
点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
13．
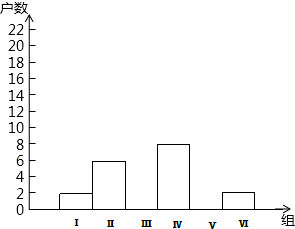今年是我国施行“清明”小长假的第二年，在长假期间，某校团委要求学生参加一项社会调查活动．九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况，从中随机调查了40户居民家庭的人均收入情况（收入取整数，单位：元）并绘制了如下的分布表和分布图：
根据以上提供的信息，解答下列问题：
（1）补全分布表、分布图；
（2）这40户家庭收入的中位数落在哪一个小组？
（3）被调查的家庭中，参加“清明扫墓“活动的家庭统计如表：
问：估计该小区共有多少户家庭参加了扫墓活动．
今年是我国施行“清明”小长假的第二年，在长假期间，某校团委要求学生参加一项社会调查活动．九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况，从中随机调查了40户居民家庭的人均收入情况（收入取整数，单位：元）并绘制了如下的分布表和分布图：| 分组 | 户数 | 百分比 |
| Ⅰ：600-799 | 2 | 0.05 |
| Ⅱ：800-999 | 6 | 0.15 |
| Ⅲ：1000-1199 | 0.45 | |
| Ⅳ：1200-1399 | 8 | 0.20 |
| Ⅴ：1400-1599 | ||
| Ⅵ：1600-1800 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
（1）补全分布表、分布图；
（2）这40户家庭收入的中位数落在哪一个小组？
（3）被调查的家庭中，参加“清明扫墓“活动的家庭统计如表：
| 收入情况 | 600-799 | 800-999 | 1000-1199 | 1200-1399 | 1400-1599 | 1600-1800 |
| $\frac{参加扫墓家庭数}{被调查家庭数}$ | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ | 1 | 1 |
14．下列等式变形正确的是（ ）
| A． | 如果s=ab，那么b=$\frac{s}{a}$ | B． | 如果x=6，那么x=3 | ||
| C． | 如果x-3=y-3，那么x-y=0 | D． | 如果mx=my，那么x=y |