题目内容
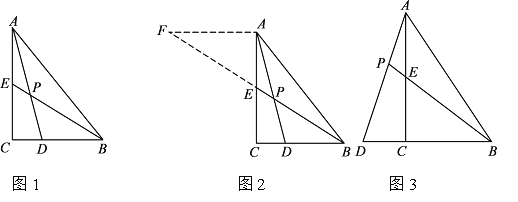
【题目】如图1,在△ABC中,AB=BC=5,AC=6,△ECD是△ABC沿BC方向平移得到的,连接AE、BE,且AC和BE相交于点O.
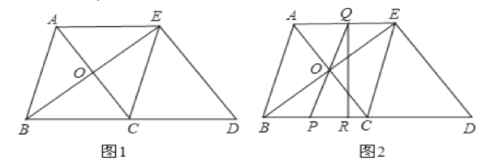
(1)求证:四边形ABCE是菱形;
(2)如图2,P是线段BC上一动点(不与B. C重合),连接PO并延长交线段AE于点Q,过Q作QR⊥BD交BD于R.
①四边形PQED的面积是否为定值?若是,请求出其值;若不是,请说明理由;
②以点P、Q、R为顶点的三角形与以点B. C. O为顶点的三角形是否可能相似?若可能,请求出线段BP的长;若不可能,请说明理由.
【答案】(1)见解析;(2)①24,②![]() ;
;
【解析】
(1)利用平移的性质以及菱形的判定得出即可;
(2)①首先过E作EF⊥BD交BD于F,则∠EFB=90°,证出△QOE≌△POB,利用QE=BP,得出四边形PQED的面积为定值;
②当∠QPR=∠BCO时,△PQR∽△CBO,此时有OP=OC=3,过O作OG⊥BC交BC于G,得出△OGC∽△BOC,利用相似三角形的性质得出CG的长,进而得出BP的长.
(1)证明:∵△ABC沿BC方向平移得到△ECD,
∴EC=AB,AE=BC,
∵AB=BC,
∴EC=AB=BC=AE,
∴四边形ABCE是菱形;
(2)①四边形PQED的面积是定值,理由如下:
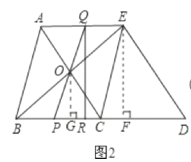
过E作EF⊥BD交BD于F,则∠EFB=90°,
∵四边形ABCE是菱形,
∴AE∥BC,OB=OE,OA=OC,OC⊥OB,
∵AC=6,
∴OC=3,
∵BC=5,
∴OB=4,sin∠OBC=![]() ,
,
∴BE=8,
∴EF=BEsin∠OBC=8×![]() ,
,
∵AE∥BC,
∴∠AEO=∠CBO,四边形PQED是梯形,
在△QOE和△POB中
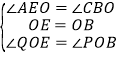 ,
,
∴△QOE≌△POB,
∴QE=BP,
∴S![]() =
=![]() (QE+PD)×EF=
(QE+PD)×EF=![]() (BP+DP)×EF=
(BP+DP)×EF=![]() ×BD×EF=
×BD×EF=![]() ×2BC×EF=BC×EF=5×
×2BC×EF=BC×EF=5×![]() =24;
=24;
②△PQR与△CBO可能相似,
∵∠PRQ=∠COB=90°,∠QPR>∠CBO,
∴当∠QPR=∠BCO时,△PQR∽△CBO,此时有OP=OC=3.
过O作OG⊥BC交BC于G.
∵∠OCB=∠OCB,∠OGC=∠BOC,
∴△OGC∽△BOC,
∴CG:CO=CO:BC,
即CG:3=3:5,
∴CG=![]() ,
,
∴BP=BCPC=BC2CG=52×![]() =
=![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的.该市电费收费标准如下表(按月结算) :
每月用电量/度 | 电价/(元/度) |
不超过 |
|
超过 |
|
超过 |
|
解答下列问题:
(1)某居民![]() 月份用电量为
月份用电量为![]() 度,请问该居民
度,请问该居民![]() 月应缴电费多少元?
月应缴电费多少元?
(2)设某月的用电量为![]() 度
度![]() ,试写出不同用电量范围应缴的电费(用
,试写出不同用电量范围应缴的电费(用![]() 表示) .
表示) .
(3)某居民![]() 月份缴电费
月份缴电费![]() 元,求该居民
元,求该居民![]() 月份的用电量.
月份的用电量.