Question

已知二次函数y＝x²－2mx＋m²－1.

(1)当二次函数的图象经过坐标原点O(0,0)时，求二次函数的解析式；

(2)如图3­4­14，当m＝2时，该抛物线与y轴交于点C，顶点为D，求C，D两点的坐标；

(3)在(2)的条件下，x轴上是否存在一点P，使得PC＋PD最短？若P点存在，求出P点的坐标；若P点不存在，请说明理由．

图3­4­14

Answer 1

解：(1)将点O(0,0)代入，解得m＝±1，

二次函数关系式为y＝x²＋2x或y＝x²－2x.

(2)当m＝2时，y＝x²－4x＋3＝(x－2)²－1，

∴D(2，－1)．当x＝0时，y＝3，∴C(0,3)．

(3)存在．接连接C，D交x轴于点P，则点P为所求．

由C(0,3)，D(2，－1)求得直线CD为y＝－2x＋3.

当y＝0时，x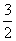＝，∴P.