题目内容
正方形ABCD中,P为AB边上任一点,AE⊥DP于E,点F在DP的延长线上,且DE=EF,连接AF、BF,∠BAF的平分线交DF于G,连接GC.(1)求证:△AEG是等腰直角三角形;
(2)求证:AG+CG=
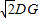 ;
;(3)若AB=2,P为AB的中点,求BF的长.
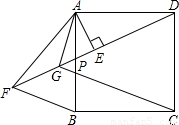
【答案】分析:(1)由条件可以得出∠F=∠PAE,再由直角三角形的性质两锐角互余及角平分线的性质就可以得出2∠GAP+2∠PAE=90°,从而求出结论;
(2)如图2,作CH⊥DP,交DP于H点,可以得出△ADE≌△DCH根据全等三角形的性质就可以得出△GHC是等腰直角三角形,由其性质就可以得出CG= GH,AG=
GH,AG=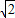 EG,再根据线段转化就看以得出结论;
EG,再根据线段转化就看以得出结论;
(3)如图3,延长DF,CB交于点K,根据正方形的性质可以得出△ADP≌△BKP,再由勾股定理就可以得出F是KG的中点,由三角形的中位线的性质就可以求出结论.
解答:(1)证明:如图1,∵DE=EF,AE⊥DP,
∴AF=AD,
∴∠F=∠ADF,
∵∠ADF+∠DAE=∠PAE+∠DAE=90°,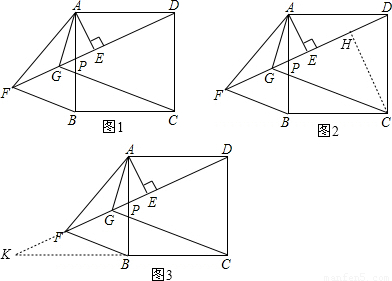
∴∠F=∠PAE,
∵DF平分∠BAF,
∴∠FAG=∠GAP.
∵∠F+∠FAE=90°,
∴∠F+∠PAE+∠FAP=90°
∴2∠GAP+2∠PAE=90°,
即∠GAE=45°,
∴△AGE为等腰直角三角形;
(2)证明:如图2,作CH⊥DP,交DP于H点,
∴∠DHC=90°.
∵AE⊥DP,
∴∠AED=90°,
∴∠AED=∠DHC.
∵∠ADE+∠CDH=90°,∠CDH+∠DCH=90°,
∴∠ADE=∠DCH.
∵在△ADE和△DCH中,
 ,
,
∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=EG.
∴EH+EG=EH+HD,
即GH=ED,
∴GH=CH.
∴CG= GH.
GH.
∵AG=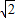 EG,
EG,
∴AG=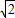 DH,
DH,
∴CG+AG=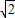 GH+
GH+ HD,
HD,
∴CG+AG=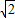 (GH+HD),
(GH+HD),
即CG+AG=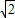 DG;
DG;
(3)如图3,延长DF,CB交于点K,
∵P是AB的中点,
∴AP=BP=1.
∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠DAB=∠ABC=∠ABK=90°.
∵在△ADP和△BKP中
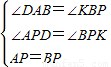 ,
,
∴△ADP≌△BKP(AAS),
∴AD=KB=BC=2.
在Rt△ADP中由勾股定理,得
PD= ,
,
∴ AE=PA•AD,
AE=PA•AD,
∴AE=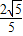 ,DE=
,DE= ,
,
∴EG=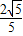 ,DF=
,DF=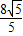 ,
,
∴FG= .
.
在Rt△KCD中,由勾股定理,得
KD=2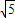 ,
,
∴KF= ,
,
∴KF=FG,
∵KB=BC,
∴FB∥CG,BF= CG,
CG,
∴BF= •
• CH=
CH=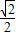 AD=
AD=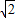 .
.
点评:本题考查了等腰三角形的性质的运用,直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,三角形的中位线的判定及性质的运用,解答时合理运用全等是重点,运用三角形的中位线的性质求解是难点.
(2)如图2,作CH⊥DP,交DP于H点,可以得出△ADE≌△DCH根据全等三角形的性质就可以得出△GHC是等腰直角三角形,由其性质就可以得出CG=
 GH,AG=
GH,AG=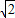 EG,再根据线段转化就看以得出结论;
EG,再根据线段转化就看以得出结论;(3)如图3,延长DF,CB交于点K,根据正方形的性质可以得出△ADP≌△BKP,再由勾股定理就可以得出F是KG的中点,由三角形的中位线的性质就可以求出结论.
解答:(1)证明:如图1,∵DE=EF,AE⊥DP,
∴AF=AD,
∴∠F=∠ADF,
∵∠ADF+∠DAE=∠PAE+∠DAE=90°,

∴∠F=∠PAE,
∵DF平分∠BAF,
∴∠FAG=∠GAP.
∵∠F+∠FAE=90°,
∴∠F+∠PAE+∠FAP=90°
∴2∠GAP+2∠PAE=90°,
即∠GAE=45°,
∴△AGE为等腰直角三角形;
(2)证明:如图2,作CH⊥DP,交DP于H点,
∴∠DHC=90°.
∵AE⊥DP,
∴∠AED=90°,
∴∠AED=∠DHC.
∵∠ADE+∠CDH=90°,∠CDH+∠DCH=90°,
∴∠ADE=∠DCH.
∵在△ADE和△DCH中,
 ,
,∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=EG.
∴EH+EG=EH+HD,
即GH=ED,
∴GH=CH.
∴CG=
 GH.
GH.∵AG=
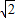 EG,
EG,∴AG=
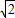 DH,
DH,∴CG+AG=
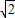 GH+
GH+ HD,
HD,∴CG+AG=
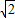 (GH+HD),
(GH+HD),即CG+AG=
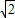 DG;
DG;(3)如图3,延长DF,CB交于点K,
∵P是AB的中点,
∴AP=BP=1.
∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠DAB=∠ABC=∠ABK=90°.
∵在△ADP和△BKP中
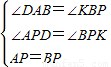 ,
,∴△ADP≌△BKP(AAS),
∴AD=KB=BC=2.
在Rt△ADP中由勾股定理,得
PD=
 ,
,∴
 AE=PA•AD,
AE=PA•AD,∴AE=
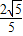 ,DE=
,DE= ,
,∴EG=
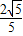 ,DF=
,DF=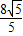 ,
,∴FG=
 .
.在Rt△KCD中,由勾股定理,得
KD=2
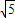 ,
,∴KF=
 ,
,∴KF=FG,
∵KB=BC,
∴FB∥CG,BF=
 CG,
CG,∴BF=
 •
• CH=
CH=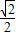 AD=
AD=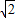 .
.点评:本题考查了等腰三角形的性质的运用,直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,三角形的中位线的判定及性质的运用,解答时合理运用全等是重点,运用三角形的中位线的性质求解是难点.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 (2013•临沂)如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
(2013•临沂)如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( ) 如图,在正方形ABCD中,画2个半径为a的四分之一圆,用代数式表示阴影部分的面积为
如图,在正方形ABCD中,画2个半径为a的四分之一圆,用代数式表示阴影部分的面积为 如图,在正方形ABCD中,AB=4,E在BC边上,BE=1,F是AC上一动点,则EF+BF的最小值是
如图,在正方形ABCD中,AB=4,E在BC边上,BE=1,F是AC上一动点,则EF+BF的最小值是