题目内容
求下图中直线L的解析式
 |
解:∵当y=0时,x=2,
∴直线y=x﹣2与x轴的交点为(2,0),
∵直线L过点(2,0),(0,3),
设直线L的解析式为y=kx+b(k≠0),
∴ ,
,
解得 ,
,
∴直线L的解析式为:y=﹣ x+3.
x+3.

练习册系列答案
相关题目
(1)如图14,矩形ABCD中,AB=5cm,BC=2cm,在AB边上取一点E,(点E与A、B 不重合),连接DE、CE,分矩形ABCD所成的3个三角形都相似.我们把这样的点E叫做矩形ABCD的AB边上的强相似点,在图12的AB边上画出满足要求的强相似点E,并求
不重合),连接DE、CE,分矩形ABCD所成的3个三角形都相似.我们把这样的点E叫做矩形ABCD的AB边上的强相似点,在图12的AB边上画出满足要求的强相似点E,并求 AE的长;(画图工具不限)
AE的长;(画图工具不限)
 |
(2)对于任意一个矩形ABCD,AB边上是否一定存在这样的强相似点E?如果一定存在,请说明理由;如果不一定存在,请举例说明;
(3)在四边形ABCD中,AD∥BC,AD<BC,∠B=90°,当点E是四边形ABCD的AB边上的一个强相似点时.
猜想:AE与BE的数量关系__________________________.
并分别给出理由.
 的值等于( )
的值等于( ) B.一2 C.? 2 D.
B.一2 C.? 2 D.

 ③ 根据①、②两题的计算结果,请猜想∠DAE与∠ABC和∠ACB之间的关系(用等式表示出来)
③ 根据①、②两题的计算结果,请猜想∠DAE与∠ABC和∠ACB之间的关系(用等式表示出来)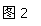

 ,则△ABC的形状是( )
,则△ABC的形状是( ) ,
, 。则求值:
。则求值: = ;
= ; = 。
= 。