题目内容
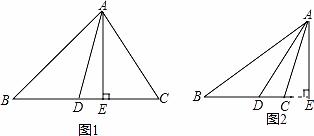
在△ABC中,AD是角平分线,AE是高线
① 如图①所示,∠ABC=40°,∠ACB=70°,求∠DAE。
② 如图②所示,∠ABC=30°,∠ACB=110°,求∠DAE。
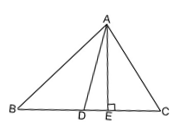
 ③ 根据①、②两题的计算结果,请猜想∠DAE与∠ABC和∠ACB之间的关系(用等式表示出来)
③ 根据①、②两题的计算结果,请猜想∠DAE与∠ABC和∠ACB之间的关系(用等式表示出来)
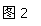

解:①∵∠ABC=40°,∠ACB=70°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=70°,
∵AD平分∠BAC,
∴∠CAD= ∠BAC=
∠BAC= ×70°=35°,
×70°=35°,
∵AE⊥BC,
∴∠AEC=90°,
∵∠C=70°,
∴∠EAC=180°﹣90°﹣70°=20°,
∴∠DAE=∠DAC﹣∠EAC=35°﹣20°=15°.
②∵∠ABC=30°,∠ACB=110°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=40°,
∵AD平分∠BAC,
∴∠CAD= ∠BAC=
∠BAC= ×40°=20°,
×40°=20°,
∵AE⊥BC,
∴∠AEC=90°,
∵∠C=110°,
∴∠EAC=∠ACB﹣∠AEC=110°﹣90°=20°,
∴∠DAE=∠DAC+∠EAC=20°+20°=40°.
③∠DAE= ∠ACB﹣
∠ACB﹣ ∠ABC,理由如下:
∠ABC,理由如下:
分为两种情况:如图1,
∠BAC=180°﹣(∠ABC+∠ACB),
∵AD平分∠BAC,
∴∠DAC= [180°﹣(∠ABC+∠ACB)]=90°﹣
[180°﹣(∠ABC+∠ACB)]=90°﹣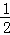 ∠ABC﹣
∠ABC﹣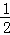 ∠ACB,
∠ACB,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣∠ACB,
∴∠DAE=∠DAC﹣∠EAC=(90°﹣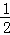 ∠ABC﹣
∠ABC﹣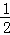 ∠ACB)﹣(90°﹣∠ACB)=
∠ACB)﹣(90°﹣∠ACB)=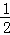 ∠ACB﹣
∠ACB﹣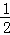 ∠ABC;
∠ABC;
如图2,
∠BAC=180°﹣∠ABC﹣∠ACB,
∵AD平分∠BAC,
∴∠CAD=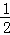 ∠BAC=
∠BAC=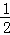 ×(180°﹣∠ABC﹣∠ACB)=90°﹣
×(180°﹣∠ABC﹣∠ACB)=90°﹣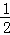 ∠ABC﹣
∠ABC﹣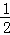 ∠ACB,
∠ACB,
∵AE⊥BC,
∴∠AEC=90°,
∴∠EAC=∠ACB﹣∠AEC=∠ACB﹣90°,
∴∠DAE=∠DAC+∠CAD=90°﹣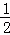 ∠ABC﹣
∠ABC﹣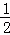 ∠ACB+∠ACB﹣90°=
∠ACB+∠ACB﹣90°=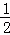 ∠ACB﹣
∠ACB﹣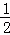 ∠ABC.
∠ABC.

 通城学典默写能手系列答案
通城学典默写能手系列答案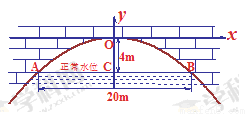

 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )
的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( ) D. x=-1
D. x=-1 , 则
, 则 =______
=______
