题目内容
B为线段OA的中点，P为以O为圆心，OB为半径的圆上的动点，当PA的中点Q落在⊙O上时，如图，则cos∠OQB的值等于
| A． | B． | C． | D． |
C解析:
解：当点P运动到恰好点Q落在⊙O上，连接QB，OP，BC，
再连接QO并延长交⊙O于点C，则∠CBQ=90°（直径所对的圆周角是直角）
∵B、Q分别是OA、AP的中点，
∴BQ∥OP，
∵OP=OB=BA=
OA=2，
∴QB=1
在Rt△CQB中，∠CBQ=90°
∴cos∠OQB="QB" QC =
故选C．
解：当点P运动到恰好点Q落在⊙O上，连接QB，OP，BC，
再连接QO并延长交⊙O于点C，则∠CBQ=90°（直径所对的圆周角是直角）
∵B、Q分别是OA、AP的中点，
∴BQ∥OP，
∵OP=OB=BA=
OA=2，∴QB=1
在Rt△CQB中，∠CBQ=90°
∴cos∠OQB="QB" QC =
故选C．
练习册系列答案
相关题目
如图，点A是函数y=| 4 |
| x |
| A、4π | B、3π | C、2π | D、π |
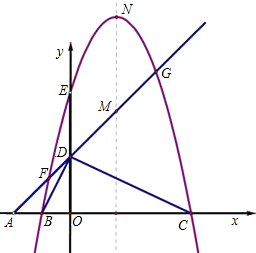如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．