题目内容
19. 如图所示,数轴上依次有三点A,O,B,点A位于原点O的左侧且相距40个单位长度,BO=30个单位长度,点P从A点出发以3个单位长度/秒的速度匀速向B点运动,点Q从B点出发,以a 个单位长度/秒的速度匀速向A点运动,两点同时出发(P、Q只在线段AB上运动).若BO表示点O与点B之间的距离,PO表示点P与点O之间的距离,QO表示点Q与点O之间的距离.
如图所示,数轴上依次有三点A,O,B,点A位于原点O的左侧且相距40个单位长度,BO=30个单位长度,点P从A点出发以3个单位长度/秒的速度匀速向B点运动,点Q从B点出发,以a 个单位长度/秒的速度匀速向A点运动,两点同时出发(P、Q只在线段AB上运动).若BO表示点O与点B之间的距离,PO表示点P与点O之间的距离,QO表示点Q与点O之间的距离.(1)2秒后点P与点Q的距离为|64-2a|;(用含a的代数式表示)
(2)当a=2时,求经过多少秒后PO=QO;
(3)当a=$\frac{9}{4}$且t≠$\frac{40}{3}$时,$\frac{PO}{QO}$的值随时间t的变化而改变吗?请说明理由.
分析 (1)先表示出2秒后P、Q两点所表示的数,再根据两点间的距离公式可得;
(2)设t秒后,PO=QO,表示出a=2时,P、Q两点所表示的数,继而由PO=QO列出关于t的方程,解之可得;
(3)表示出a=$\frac{9}{4}$且t≠$\frac{40}{3}$时PO、QO的长,由$\frac{PO}{QO}=\frac{|-40+3t|}{|30-\frac{9}{4}t|}$=$\frac{|3t-40|}{|-\frac{3}{4}|•|3t-40|}$=$\frac{4}{3}$可得答案.
解答 解:(1)2秒后点P表示数-40+2×3=-34,点Q表示数30-2a,
则PQ=|30-2a-(-34)|=|64-2a|,
故答案为:|64-2a|;
(2)设t秒后,PO=QO,
当a=2时,点P表示数-40+3t,点Q表示30-2t,
根据题意知,|-40+3t|=|30-2t|,
解得:t=14或t=10,
答:经过10秒或14秒后PO=QO;
(3)当a=$\frac{9}{4}$时,点P表示数-40+3t,点Q表示数30-$\frac{9}{4}$t,
则PO=|-40+3t|、QO=|30-$\frac{9}{4}$t|,
∵t≠$\frac{40}{3}$,
∴$\frac{PO}{QO}=\frac{|-40+3t|}{|30-\frac{9}{4}t|}$=$\frac{|3t-40|}{|-\frac{3}{4}|•|3t-40|}$=$\frac{4}{3}$,
故当a=$\frac{9}{4}$且t≠$\frac{40}{3}$时,$\frac{PO}{QO}$的值不随时间t的变化而改变.
点评 本题主要考查数轴、两点间的距离公式及一元一次方程的应用,根据两点间的距离公式表示出所需线段的长度是解题的关键.

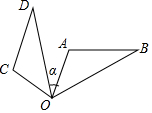 如图,△OAB绕点O逆时针旋转70°得到△OCD,若∠A=110°,∠D=30°,则∠α的度数是( )
如图,△OAB绕点O逆时针旋转70°得到△OCD,若∠A=110°,∠D=30°,则∠α的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
 如图,将△ABC绕着点C顺时针旋转50°后得到△DEC.若∠A=40°,∠E=110°,则∠BCD的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△DEC.若∠A=40°,∠E=110°,则∠BCD的度数是( )| A. | 110° | B. | 80° | C. | 40° | D. | 30° |
| A. | -8或1 | B. | 8 | C. | -8或2 | D. | 2 |
| A. | 最大的负有理数是-1 | |
| B. | 任何有理数的绝对值都是正数 | |
| C. | 0是最小的数 | |
| D. | 如果两个数互为相反数,那么它们的绝对值相等 |
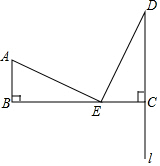 如图,AB=3,BC=8,AB⊥BC,l⊥BC于点C,点E从B向C运动,过点E作ED⊥AE,交l于D.
如图,AB=3,BC=8,AB⊥BC,l⊥BC于点C,点E从B向C运动,过点E作ED⊥AE,交l于D.