题目内容
用棋子按规律摆出下列一组图形:
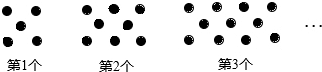
(1)填写如表:
(2)照这样的方式摆下去,则第n个图形中棋子的枚数是 ;
(3)有同学认为其中某个图形中有2015枚棋子,你认为对吗?说明你的理由.

(1)填写如表:
| 图形编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 图中棋子数 | 5 | 8 | 11 |
(3)有同学认为其中某个图形中有2015枚棋子,你认为对吗?说明你的理由.
考点:规律型:图形的变化类
专题:
分析:(1)首先观察图形数出每个图形的枚数,分别是5,8,11,…,分分析总结得出每个比前一个多3个,根据此填表,
(2)由(1)得到一个首项为5,公差为3的等差数列,由此可写出摆第n个图形所需棋子的枚数.
(3)根据(2)得出的代数式判断某一图形可能共有2015枚棋子是否可能.
(2)由(1)得到一个首项为5,公差为3的等差数列,由此可写出摆第n个图形所需棋子的枚数.
(3)根据(2)得出的代数式判断某一图形可能共有2015枚棋子是否可能.
解答:解:(1)填写如表:
(2)图中棋子数是首项为5,公差为3的等差数列,
所以摆第n个图形所需棋子的枚数为:5+3(n-1)=3n+2.
(3)我认为正确.
假设第n个图形中共有2015枚棋子,依题意得
2+3n=2015
解得:n=671.
| 图形编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 图中棋子数 | 5 | 8 | 11 | 14 | 17 | 20 |
所以摆第n个图形所需棋子的枚数为:5+3(n-1)=3n+2.
(3)我认为正确.
假设第n个图形中共有2015枚棋子,依题意得
2+3n=2015
解得:n=671.
点评:此题考查图形的变化规律,找出图形之间的联系,得出规律,解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从下列物体抽象出来的几何体可以看成圆柱的是( )
A、 |
B、 |
C、 |
D、 |
 小青从如图所示几何体,她看到的平面图形是( )
小青从如图所示几何体,她看到的平面图形是( )A、 |
B、 |
C、 |
D、 |
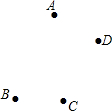 作图题:已知平面上点A,B,C,D.按下列要求画出图形:
作图题:已知平面上点A,B,C,D.按下列要求画出图形: 已知
已知
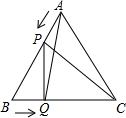 如图,P、Q是边长为6cm的等边△ABC边AB、BC上两动点,点P从点A,点Q从点B同时出发,运动时间为t秒,速度是1cm/s,则当△BPQ是直角三角形时,t的值是
如图,P、Q是边长为6cm的等边△ABC边AB、BC上两动点,点P从点A,点Q从点B同时出发,运动时间为t秒,速度是1cm/s,则当△BPQ是直角三角形时,t的值是 如图,AB∥CD∥EF∥GH,AC:CE:EG=2:3:4,BD=3,则BH=
如图,AB∥CD∥EF∥GH,AC:CE:EG=2:3:4,BD=3,则BH= 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,0)、B(-1,-2)、C(-2,2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,0)、B(-1,-2)、C(-2,2).