题目内容
18.下列函数中和函数$y=\frac{1}{x-1}$的图象关于y轴对称的( )| A. | $y=\frac{1}{x+1}$ | B. | $y=-\frac{1}{x+1}$ | C. | $y=\frac{1}{1-x}$ | D. | $y=\frac{1}{x-1}$ |
分析 取$y=\frac{1}{x-1}$的图象任意一点(x,y),再写出这个点关于y轴的对称点,然后通过判断点(-x,y)是否满足四个选项中的解析式得到正确答案.
解答 解:设点(x,y)为$y=\frac{1}{x-1}$的图象上一点,
点(x,y)关于y轴的对称点为(-x,y),
而点(-x,y)满足y=-$\frac{1}{x+1}$,
所以y=-$\frac{1}{x+1}$和函数$y=\frac{1}{x-1}$的图象关于y轴对称.
故选B.
点评 本题考查了反比例函数的性质:反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
7.下列式子:$\sqrt{{{(-3)}^2}},\sqrt{-5},\sqrt{8},\sqrt{{a^2}-1},\sqrt{{a^2}+1},\sqrt{4-4a+{a^2}},\root{3}{5}$中,一定是二次根式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.$\frac{2m}{m+n}$-$\frac{m-n}{n+m}$的运算结果是( )
| A. | $\frac{3m-n}{n+m}$ | B. | -$\frac{3m-n}{n+m}$ | C. | $\frac{m-n}{m+n}$ | D. | 1 |
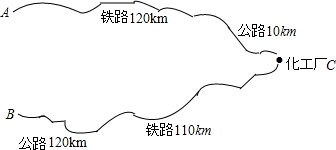 如图,某化工厂C与A、B两地有公路、跌路相连.这家工厂从A地购买一批每吨1000元的原料回工厂,制成若干每吨8000元的产品运回B地.已知公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),若这两次运输共支出铁路运费97200元,且这批产品的销售款比原料费与运输费的和多1887800元.这两次运输共支出公路运输费多少元?
如图,某化工厂C与A、B两地有公路、跌路相连.这家工厂从A地购买一批每吨1000元的原料回工厂,制成若干每吨8000元的产品运回B地.已知公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),若这两次运输共支出铁路运费97200元,且这批产品的销售款比原料费与运输费的和多1887800元.这两次运输共支出公路运输费多少元?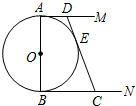 如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN 于C.设AD=x,BC=y.
如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN 于C.设AD=x,BC=y.