题目内容
1.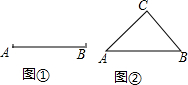 如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.(1)请用直尺和圆规在图①中画一个以AB为边的“好玩三角形”;
(2)如图②,在Rt△ABC中,∠C=90°,$\frac{BC}{AC}=\frac{\sqrt{3}}{2}$,求证:△ABC是“好玩三角形”.
分析 (1)先作AB的垂直平分线得到AB的中点D,然后以D为端点任意画线段CD=AB,再连结AC、BC,则△ACB满足条件;
(2)取AC的中点D,连结BD,如图②,设AC=2x,则CD=AD=x,利用$\frac{BC}{AC}=\frac{\sqrt{3}}{2}$得到BC=$\sqrt{3}$x,再在Rt△BCD中利用勾股定理计算出BD=2x,则BD=AC,然后根据“好玩三角形”即可得到结论.
解答 (1)解:如图①,△ABC为所作;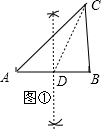
(2)证明:取AC的中点D,连结BD,如图②,
设AC=2x,则CD=AD=x,
∵$\frac{BC}{AC}=\frac{\sqrt{3}}{2}$,
∴BC=$\sqrt{3}$x,
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{(\sqrt{3}x)^{2}+{x}^{2}}$=2x,
∴BD=AC,
∴△ABC是“好玩三角形”.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
6.多项式x2-1与多项式x2-2x+1的公因式是( )
| A. | x-1 | B. | x+1 | C. | x2-1 | D. | (x-1)2 |
 (1)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DAO.
(1)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DAO. 如图,直线l上有A、B两点,AB=24cm,点O是线段AB上的一点,OA=2OB.
如图,直线l上有A、B两点,AB=24cm,点O是线段AB上的一点,OA=2OB.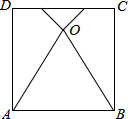 如图,将正方形ABCD的边AD和边BC折叠,使点C与点D重合于正方形内部一点O,已知点O到边CD的距离为a,则点O到边AB的距离为(3+2$\sqrt{3}$)a.(用a的代数式表示)
如图,将正方形ABCD的边AD和边BC折叠,使点C与点D重合于正方形内部一点O,已知点O到边CD的距离为a,则点O到边AB的距离为(3+2$\sqrt{3}$)a.(用a的代数式表示)