题目内容
对于每个正整数n,关于x的一元二次方程x2-
x+
=0的两个根分别为an、bn,设平面直角坐标系中,An、Bn两点的坐标分别为An(an,0),Bn(bn,0),AnBn表示这两点间的距离,则AnBn=______(用含n的代数式表示);A1B1+A2B2+…+A2012B2012的值为______.
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
∵关于x的一元二次方程x2-
x+
=0的两个根分别为an、bn,
∴AnBn=
=
=
;
∴A1B1+A2B2+…+A2012B2012
=
+
+…+
=1-
+
-
+…+
-
=1-
=
.
故答案为
、
.
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
∴AnBn=
| ||||||
| 1 |
|
| 1 |
| n(n+1) |
∴A1B1+A2B2+…+A2012B2012
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2011×2012 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2011 |
| 1 |
| 2012 |
=1-
| 1 |
| 2012 |
=
| 2011 |
| 2012 |
故答案为
| 1 |
| n(n+1) |
| 2011 |
| 2012 |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
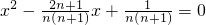 的两个根分别为an、bn,设平面直角坐标系中,An、Bn两点的坐标分别为An(an,0),Bn(bn,0),AnBn表示这两点间的距离,则AnBn=________(用含n的代数式表示);A1B1+A2B2+…+A2012B2012的值为________.
的两个根分别为an、bn,设平面直角坐标系中,An、Bn两点的坐标分别为An(an,0),Bn(bn,0),AnBn表示这两点间的距离,则AnBn=________(用含n的代数式表示);A1B1+A2B2+…+A2012B2012的值为________.