题目内容
对于每个正整数n,关于x的一元二次方程x2-
x+
=0的两个根分别为an、bn,设平面直角坐标系中,An、Bn两点的坐标分别为An(an,0),Bn(bn,0),AnBn表示这两点间的距离,则AnBn=
(用含n的代数式表示);A1B1+A2B2+…+A2012B2012的值为
.
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
| 1 |
| n(n+1) |
| 1 |
| n(n+1) |
| 2011 |
| 2012 |
| 2011 |
| 2012 |
分析:由于关于x的一元二次方程x2-
x+
=0的两个根分别为an、bn,可知,二次函数y=x2-
x+
与x轴的交点间的距离为
,据此求出AnBn的表达式,然后令n=1,n=2,…,据此列出A1B1+A2B2+…+A2012B2012的表达式,计算即可.
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
| ||
| |a| |
解答:解:∵关于x的一元二次方程x2-
x+
=0的两个根分别为an、bn,
∴AnBn=
=
=
;
∴A1B1+A2B2+…+A2012B2012
=
+
+…+
=1-
+
-
+…+
-
=1-
=
.
故答案为
、
.
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
∴AnBn=
| ||||||
| 1 |
|
| 1 |
| n(n+1) |
∴A1B1+A2B2+…+A2012B2012
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2011×2012 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2011 |
| 1 |
| 2012 |
=1-
| 1 |
| 2012 |
=
| 2011 |
| 2012 |
故答案为
| 1 |
| n(n+1) |
| 2011 |
| 2012 |
点评:本题考查了一元二次方程与二次函数的关系,以及二次函数与x轴交点间的距离公式,同时要进行规律探究,难度较大.

练习册系列答案
相关题目
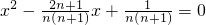 的两个根分别为an、bn,设平面直角坐标系中,An、Bn两点的坐标分别为An(an,0),Bn(bn,0),AnBn表示这两点间的距离,则AnBn=________(用含n的代数式表示);A1B1+A2B2+…+A2012B2012的值为________.
的两个根分别为an、bn,设平面直角坐标系中,An、Bn两点的坐标分别为An(an,0),Bn(bn,0),AnBn表示这两点间的距离,则AnBn=________(用含n的代数式表示);A1B1+A2B2+…+A2012B2012的值为________.