题目内容
对于每个正整数n,抛物线y=x2-| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
AnBn=
分析:根据抛物线的解析式,抛物线与x轴交点的横坐标,一个是
,另一个是
,根据x轴上两点间的距离公式,得AnBn=
-
,再代入计算即可.
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:∵抛物线的解析式为y=x2-
x+
,
∴抛物线与x轴交点坐标为(
,0),(
,0),
∴AnBn=
-
,
∴A1B1+A2B2+…+A2011B2011=1-
+
-
+…+
-
=1-
=
,
故答案为
.
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
∴抛物线与x轴交点坐标为(
| 1 |
| n |
| 1 |
| n+1 |
∴AnBn=
| 1 |
| n |
| 1 |
| n+1 |
∴A1B1+A2B2+…+A2011B2011=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2011 |
| 1 |
| 2012 |
=1-
| 1 |
| 2012 |
=
| 2011 |
| 2012 |
故答案为
| 2011 |
| 2012 |
点评:本题是一道找规律的题目,考查了抛物线与x轴的交点问题,令y=0,方程的两个实数根正好是抛物线与x轴交点的横坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
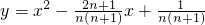 与x轴交于An,Bn两点,若AnBn表示这两点间的距离,则
与x轴交于An,Bn两点,若AnBn表示这两点间的距离,则 与x轴交于An,Bn两点,若AnBn表示这两点间的距离,则
与x轴交于An,Bn两点,若AnBn表示这两点间的距离,则 与x轴交于An,Bn两点,若AnBn表示这两点间的距离,则
与x轴交于An,Bn两点,若AnBn表示这两点间的距离,则