题目内容
如图所示,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( )
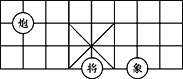
A. (1,3) B. (-2,0) C. (-1,2) D. (-2,2)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
如图所示,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( )

A. (1,3) B. (-2,0) C. (-1,2) D. (-2,2)
 名校课堂系列答案
名校课堂系列答案