题目内容
2.(1)当a=$\frac{1}{2}$,b=$\frac{1}{3}$时,分别求代数式a2-2ab+b2?(a-b)2的值;(2)当a=-5,b=-3时,分别求代数式a2-2ab+b2?(a-b)2?的值;
(3)观察(1)(2)中代数式的值,a2-2ab+b2与(a-b)2有何关系?
(4)利用你发现的规律,求12.572-2×12.57×2.57+2.572的值.
分析 (1)(2)把数值分别代入代数式求得答案即可;
(3)比较计算结果得出两个代数式的关系即可;
(4)利用(3)的规律计算得出答案即可.
解答 解:(1)当a=$\frac{1}{2}$,b=$\frac{1}{3}$时,
a2-2ab+b2=$\frac{1}{36}$,(a-b)2=$\frac{1}{36}$;
(2)当a=-5,b=-3时,
a2-2ab+b2=4,(a-b)2=4;
(3)由(1)(2)可得a2-2ab+b2=(a-b)2;
(4)12.572-2×12.57×2.57+2.572
=(12.57-2.57)2
=100.
点评 本题考查了代数式求值,是基础题,准确进行计算是解题的关键,计算时要注意符号的处理.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.已知-2xm+1y3与$\frac{1}{3}$x2yn-1是同类项,则m,n的值分别为( )
| A. | m=1,n=4 | B. | m=1,n=3 | C. | m=2,n=4 | D. | m=2,n=3 |
12.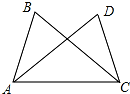 如图,已知AB=CD,那么添加下列条件后,仍不能说明△ABC≌△CDA的是( )
如图,已知AB=CD,那么添加下列条件后,仍不能说明△ABC≌△CDA的是( )
 如图,已知AB=CD,那么添加下列条件后,仍不能说明△ABC≌△CDA的是( )
如图,已知AB=CD,那么添加下列条件后,仍不能说明△ABC≌△CDA的是( )| A. | ∠BAC=∠DCA | B. | BC=DA | C. | ∠D=∠B=90° | D. | ∠BAC=∠DAC |
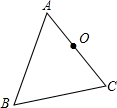 如图所示,按要求作出下列图形:
如图所示,按要求作出下列图形: 如图,D为△ABC的边AC上一点,满足AD=2CD,G为BD的中点,AG的延长线交BC于点E.求BE:EC的值.
如图,D为△ABC的边AC上一点,满足AD=2CD,G为BD的中点,AG的延长线交BC于点E.求BE:EC的值.