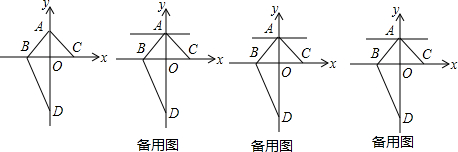
题目内容
8．4个不同整数的积是6，那么这4个整数的和是1或-1．分析 根据有理数的乘法写出6的算式，从而确定出这四个不同的整数，再根据有理数的加法运算法则进行计算即可得解．
解答 解：∵（-1）×1×（-2）×3=6，
∴这四个不同的整数为-1、1、-2、3，
它们的和=-1+1+（-2）+3=1，
∵（-1）×1×2×（-3）=6，
∴这四个不同的整数为-1、1、2、-3，
它们的和=-1+1+2+（-3）=-1，
综上所述，这4个整数的和是1或-1．
故答案为：1或-1．
点评 本题考查了有理数的乘法，有理数的加法，是基础题，难点在于确定出乘积是6的算式．
练习册系列答案
阅读快车系列答案
相关题目
19．|a|+a=2a，则a是（ ）
| A． | 0 | B． | 负数 | C． | 非负数 | D． | 正数 |
16．下列调查中，最适宜采取普查的（ ）
| A． | 一批洗衣机的使用寿命 | |
| B． | 了解某市中学生课外阅读的情况 | |
| C． | 《新闻联播》电视栏目的收视率 | |
| D． | 调查乘坐飞机的旅客是否携带了危禁物品 |
3．如图所示的运算程序中，若开始输入的x值为96，我们发现第一次输出的结果为48，第二次输出的结果为24，…，则第2013次输出的结果为（ ）
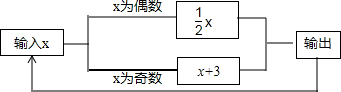
| A． | 6 | B． | 3 | C． | $\frac{3}{{2}^{2008}}$ | D． | 6027 |
20．
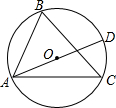如图，∠BAC=60°，AD为⊙O的直径，AD交BC于E，且BE=2CE，则$\frac{AB}{AD}$的值（ ）
如图，∠BAC=60°，AD为⊙O的直径，AD交BC于E，且BE=2CE，则$\frac{AB}{AD}$的值（ ）| A． | 2 | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{1}{2}$ |
17．
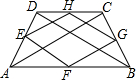如图，四边形ABCD中，AB∥DC，E，F，G，H分别是各边的中点，分别记四边形ABCD和EFGH的面积为S1和S2，则下列各个判断中正确的是（ ）
如图，四边形ABCD中，AB∥DC，E，F，G，H分别是各边的中点，分别记四边形ABCD和EFGH的面积为S1和S2，则下列各个判断中正确的是（ ）| A． | S1＞2S2 | B． | 2S1＜S2 | C． | S1=2S2 | D． | $\sqrt{{S}_{1}}$=2$\sqrt{{S}_{2}}$ |