题目内容
已知点P(a,-b)在第一象限,则直线y=ax+b经过的象限为 .
考点:一次函数图象与系数的关系,点的坐标
专题:数形结合
分析:先根据第一象限点的坐标特征得到a>0,b<0,然后根据一次函数与系数的关系判断直线y=ax+b经过的象限.
解答:解:∵P(a,-b)在第一象限,
∴a>0,-b>0,即b<0,
∴直线y=ax+b经过第一、三、四象限.
故答案为第一、三、四象限.
∴a>0,-b>0,即b<0,
∴直线y=ax+b经过第一、三、四象限.
故答案为第一、三、四象限.
点评:本题考查了一次函数与系数的关系:一次函数y=kx+b,①k>0,b>0?y=kx+b的图象在一、二、三象限;②k>0,b<0?y=kx+b的图象在一、三、四象限;③k<0,b>0?y=kx+b的图象在一、二、四象限;④k<0,b<0?y=kx+b的图象在二、三、四象限.

练习册系列答案
相关题目
计算(-3)×(4-12),用分配律计算过程正确的是( )
| A、(-3)×4+(-3)×(-12) |
| B、(-3)×4-(-3)×(-12) |
| C、3×4-(-3)×(-12) |
| D、(-3)×4+3×(-12) |
 如图:AB=AD,∠BAD=∠CAE,要添加一个条件使△ABC≌△ADE,添加的条件可以是(只写一个)
如图:AB=AD,∠BAD=∠CAE,要添加一个条件使△ABC≌△ADE,添加的条件可以是(只写一个)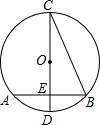 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2